设 a, b, c ∈ R, a + b + c = 0, abc = 1.
(1) 证明: ab + bc + ca < 0;
(2) 用 max{a, b, c} 表示 a, b, c 的最大值, 证明: max{a, b, c} ⩾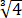 .
.
设 a, b, c ∈ R, a + b + c = 0, abc = 1.
(1) 证明: ab + bc + ca < 0;
(2) 用 max{a, b, c} 表示 a, b, c 的最大值, 证明: max{a, b, c} ⩾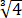 .
.
(1) 由题设可知, a, b, c 均不为零, 所以ab + bc + ca = 1/2[(a+b+c)2-(a2+b2+c2)] =-1/2(a2+b2+c2) < 0.(2) 不妨设 max{a, b, c} = a...
查看完整答案在复素数的平面图上,解不等式|(2x-1)/(x-2)|<1.
若 x, y 满足约束条件 则 z = x + 7y 的最大值为 __________.
已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.
f(x) =| x − a2 |+ |x − 2a + 1| .(1) 当 a = 2 时, 求不等式 f(x) ⩾ 4 的解集.(2) f(x) ⩾ 4, 求 a 的取值范围.
若 x, y 满足约束条件 , 则 z = x + 2y 的最大值是__________.
若正数a,b满足ab=a+b+3,则ab的取值范围是__________.
若a>b>1,p=,Q=(lga+lgb),R=lg((a+b)/2),则【 】
设函数f(x)= - ax,其中a>0.(I)解不等式f(x)≤1;(II)求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数.