已知a,b,c为正数,且a3/2+b3/2+c3/2=1.证明:
(1)abc≤1/9;
(2) a/(b+c)+b/(a+c)+c/(a+b)≤1/(2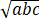 ).
).
已知a,b,c为正数,且a3/2+b3/2+c3/2=1.证明:
(1)abc≤1/9;
(2) a/(b+c)+b/(a+c)+c/(a+b)≤1/(2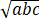 ).
).
(1)∵a,b,c为正数,∴a3/2+b3/2+c3/2≥3=3,当a=b=c=3-2/3时取等号,∴3√abc≤1,即abc≤1/9.(2)∵a,b,c为正数,∴a+b≥2√ab,b+c≥2√bc,a+c≥2√ac,当且仅当a=b=c=3-2/3时,取等号,∴(a3/2 √bc)/(b...
查看完整答案