设an=
+
+⋯+
(n=1,2,⋯).
(Ⅰ) 证明不等式n(n+1)/2<an<(n+1)2/2对所有的正整数n都成立.
(Ⅱ) 设bn<an/[n(n+1)](n=1,2,⋯)，用极限定义证明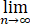
bn =1/2.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
关注优题吧，注册平台账号.
设an=++⋯+ (n=1,2,⋯).
(Ⅰ) 证明不等式n(n+1)/2<an<(n+1)2/2对所有的正整数n都成立.
(Ⅱ) 设bn<an/[n(n+1)](n=1,2,⋯)，用极限定义证明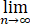bn =1/2.
证明：(Ⅰ)用数学归纳法.当n=1时，由于a1==√2，(1∙2)/2=1< 及 (1+1)2/2=2>知不等式成立.假设当n=k(k≥1)时不等式成立，即(k(k+1))/2<ak<(k+1)2/2.当n=k+1时，可得ak+1=ak+ >ak+(k+1) >(k(k+1))/2+(k+1) =((k+1)[(k+1)+1])/2.ak+1=ak+ <ak+((k+1)+(k+2...
查看完整答案