-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
高考2024年上海市( )
已知x∈R，则不等式x²-2x-3<0的解集为________.
{x|-1<x<3}
高考2024年全国甲·理( )
实数a,b满足a+b≥3.
(1)证明：2a²+2b²>a+b;
(2)证明：|a-2b² |+|b-2a² |≥6.
解答过程见word版
高考2024年全国甲·理( )
若x,y满足约束条件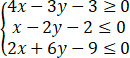
，则z=x-5y的最小值为【 】
A、1/2
B、0
C、-5/2
D、-7/2
-7/2
解答过程见word版
竞赛2024年东南地区奥林匹克( )
设a,b,c,d∈(0,1)，满足a²+b²+c²+d²=3，证明：
(1-a²)/(b+c)+(1-b²)/(c+d)+(1-c²)/(d+a)+(1-d²)/(a+b)<2/3.
解答过程见word版
竞赛2024年东南地区奥林匹克( )
若实数τ满足：对任意正整数x,y,z，均有
x²+2y²+4z²+8≥2x(y+z+τ)
则称τ为“平生数”.记最大的平生数为τ0.
(1)求τ0的值；
(2)求方程x²+2y²+4z²+8=2x(y+z+τ0)的所有正整数解(x,y,z).
首先，取x=4,y=2,z=1，有16+8+4+8≥8(2+1+τ)，得τ≤3/2.
当τ=3/2时，
x²+2y²+4z²+8-2x(y+z+3/2)
=(x-y-z-3/2)²+(y-z-3/2)²+2(z-3/2)²-1
≥1/4+1/4+1/2-1=0
等号当且仅当|x-y-z-3/2|=|y-z-3/2|=|z-3/2|=1/2时成立.
从而(x,y,z)有8组正整数解：
(4,2,1),(5,2,1),(5,3,1),(6,3,1),(6,3,2),(7,3,2),(7,4,2),(8,4,2).