高中数学-高考试题(全国甲·理 2024年线性规划问题)

单项选择（2024年全国甲·理；2024年全国甲·文）

若x,y满足约束条件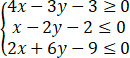，则z=x-5y的最小值为【】

A、1/2

B、0

C、-5/2

D、-7/2

答案解析

D

【解析】

解答过程见word版

讨论

高中数学

集合A={1,2,3,4,5,9},B={x|√x∈A}，则CA (A∩B)=【】

设z=5+i，则i(z ̅+z)=【】

已知双曲线C:x²-y²=m(m>0).点P1 (5,4)在C上，k为常数，0<k<1.按照如下方式依次构造点Pn (n=2,3,⋯)，过点Pn-1作斜率为k的直线与C的左支交点Qn-1，令Pn为Qn-1关于y轴的对称点，记Pn的坐标为(xn,yn).(1)若k=1/2，求x2,y2.(2)证明：数列{xn-yn}为公比为(1+k)/(1-k)的等比数列.(3)设Sn为△Pn Pn+1 Pn+2的面积，证明：对任意的正整数n,Sn=Sn+1.

某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下：第一阶段由参赛队中一名队员投篮3次,若3次都未投中则该队被淘汰,比赛成绩为0分.若至少投中一次，则该队进入第二阶段，由该队的另名队员投篮3次，每次投中得5分未投中得 0分，该队的比赛成绩为第二阶段的得分总和.某参赛队由甲、乙两名队员组成，设甲每次投中的概率为p,乙每次投中的概率为q,各次投中与否相互独立.(1)若p=0.4,q=0.5, 甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.(2)假设0<p<q.(i)为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段的比赛?(ii)为使得甲、乙所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段的比赛?

如图，平面四边形ABCD中，AB=8,CD=3,AD=5√3,∠ADC=90°,∠BAD=30°，点E,F满足(AE)→=2/5 (AD)→,(AF)→=1/2 (AB)→.将△AEF沿EF翻折至△PEF，使得PC=4√3.(1)证明：EF⊥PD;(2)求面PCD与面PBF所成二面角的正弦值.

用f(n)表示整数n的二进制中数码“1”占所有数码的比例，例如21=(10101)2，则f(21)=3/5.(1)是否存在由21个不超过2024的正整数构成的非常值等差数列a1,a2,⋯,a21，使得f(a1)=f(a2)=⋯=f(a21)？证明你的结论.(2)是否存在无穷多个正整数m，使得f(m²)>7/10？证明你的结论.

设m,n为正整数且m≤n，证明：≤m/n

设n为正整数.若平面中存在两点A,B及2024个不同的点P1,P2,⋯,P2024满足：线段AB及各条线段APi,BPi (i=1,2,⋯,2024)的长度均为不超过n的正整数，求n的最小值.

如图，在△ABC中，AB>AC,△ABC的内切圆I分别切边BC,CA,AB于点D,E,F.设M为DE的中点，N为DF的中点，直线EF与BC相交于点P，过点P作动直线l交内切圆I于不同的两点G,H,且I,M,G和I,N,H均不共线，△IMG的外接圆与△INH的外接圆交于不同于I的点Q,证明：点Q始终在一个定圆上.

有红、黄、蓝3种不同颜色的帽子各足够多顶.一个游戏团队有n(n≥4)个人,每人都知晓团队的人数为n，帽子的颜色有红、黄、蓝3种可能. 他们围成一圈进行如下游戏：步骤1：AI给每个人分配一顶帽子，每人都看不到自己的帽子，只能看到与自己相邻的两人(即顺时针、逆时针离他最近的人)的帽子；步骤2：所有人同时猜自己的帽子颜色，只要有一个人猜对，就视作游戏团队获胜;若所有人都猜错，则AI获胜.游戏团队可在步骤1之前约定猜帽子颜色的策略.(1) n=4时，游戏团队是否有必胜策略？证明你的结论；(2) n=9999时，游戏团队是否有必胜策略？证明你的结论.

线性规划问题

若实数x,y满足，则z=x-1/2 y的最小值是【】

若x,y满足约束条件，则z=2x-y的最大值是【】

若实数x,y满足约束条件，则z=3x+4y的最大值是【】

已知，则z=x+2y的最小值是________.

若 x, y 满足约束条件 , 则 z = x + 2y 的最大值是__________.

若 x, y 满足约束条件, 则 z = 3x + 2y 的最大值是__________.

若 x, y 满足约束条件则 z = x + 7y 的最大值为 __________.

记Sn为等差数列{an}的前n项和. 已知S5=S10,a5=1，则a1=【】

已知双曲线的两个焦点分别为(0,4),(0,-4)，点(-6,4)在该双曲线上，则该双曲线的离心率为【】

设函数f(x)=(ex+2sinx)/(1+x²)，则曲线y=f(x)在点(0,1)处的切线与两坐标轴所围成的三角形的面积为【】

不等式

若实数τ满足：对任意正整数x,y,z，均有x²+2y²+4z²+8≥2x(y+z+τ)则称τ为“平生数”.记最大的平生数为τ0.(1)求τ0的值；(2)求方程x²+2y²+4z²+8=2x(y+z+τ0)的所有正整数解(x,y,z).

设a,b,c,d∈(0,1)，满足a²+b²+c²+d²=3，证明：(1-a²)/(b+c)+(1-b²)/(c+d)+(1-c²)/(d+a)+(1-d²)/(a+b)<2/3.

实数a,b满足a+b≥3.(1)证明：2a²+2b²>a+b;(2)证明：|a-2b² |+|b-2a² |≥6.

湖南省二元一次不等式组

若a,b是任意实数，且a>b，则【】

不等式组的解集是【】

设函数f(x)= - ax,其中a>0.(I)解不等式f(x)≤1;(II)求a的取值范围，使函数f(x）在区间[0，+∞)上是单调函数.

若x,y满足约束条件，则z=3x+y的最小值为【】

已知实数x,y满足，则z=x-y的最大值为__________.

已知x1,y1,x2,y2,x3,y3同时满足①x1<y1,x2<y2,x3<y3；②x1+y1=x2+y2=x3,y3；③x1 y1+x3 y3=2x2 y2，以下选项恒成立的是【】