在直角坐标系 xOy 中, 曲线 C 的参数方程为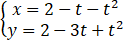 (t 为参数且 t ≠ 1), C 与坐标轴交于 A, B 两点.
(t 为参数且 t ≠ 1), C 与坐标轴交于 A, B 两点.
(1) 求 |AB|;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 求直线 AB 的极坐标方程.
在直角坐标系 xOy 中, 曲线 C 的参数方程为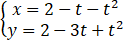 (t 为参数且 t ≠ 1), C 与坐标轴交于 A, B 两点.
(t 为参数且 t ≠ 1), C 与坐标轴交于 A, B 两点.
(1) 求 |AB|;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 求直线 AB 的极坐标方程.
(1) 因为 t≠1, 由 2 − t − t2 = 0 得 t = −2, 所以 C 与 y 轴的交点为 (0, 12); 由 2 − 3t + t2 = 0 得 t = 2,所以 C 与 x 轴的交点为 (−4, 0). 故 |AB...
查看完整答案