在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程ρ=2 cosθ.
cosθ.
(1)将C的极坐标方程化为直角坐标方程;
(2)设点A的直角坐标为(1,0),M为C上的动点,点P满足 =
=
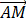 ,写出P的轨迹C1的参数方程,并判断C与C1是否有公共点.
,写出P的轨迹C1的参数方程,并判断C与C1是否有公共点.
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程ρ=2 cosθ.
cosθ.
(1)将C的极坐标方程化为直角坐标方程;
(2)设点A的直角坐标为(1,0),M为C上的动点,点P满足 =
=
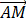 ,写出P的轨迹C1的参数方程,并判断C与C1是否有公共点.
,写出P的轨迹C1的参数方程,并判断C与C1是否有公共点.
(1)由曲线C的极坐标方程ρ=2 cosθ可得ρ2=2 ρcosθ⟺x2+y2=2 x,所以曲线C的直角坐标方程为:(x-)2+y2=2.(2)设P(x1,y1 ),则=(x1-1,y1 ),=1/ =(,)∴=+=(,)又M为C上,所以(-)2+(...
查看完整答案