高中数学-坐标系*

在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=ρcosθ+1.

(1)写出C的直角坐标方程；

(2)设直线l: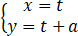(t为参数)，若C与l相交于A,B两点，且|AB|=2，求a.

解答过程见word版

试论下列函数并绘其图形

ρ = 2(1 - cosθ)

Find the equation in polar coordinates of the straight line which is perpendicular to the polar axes at a distance of 5 units from the pole.

在直角坐标系xOy中，曲线C的方程为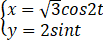（t为参数）.以坐标原点为极点，x轴正半轴为极轴建立坐标系，已知直线l的极坐标方程为ρsin⁡(θ+π/3)+m=0.

(1) 写出l的直角坐标方程；

(2) 若l与C有公共点，求m的取值范围.

(1)由ρ sin⁡(θ+π/3)+m=0可得ρ(sinθ cos⁡π/3+cosθ sin⁡π/3 )+m=0，

即ρ(1/2 sinθ+√3/2 cosθ)+m=0,1/2 y+√3/2 x+m=0,

故l的方程为√3 x+y+2m=0.

(2)由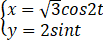得，x=√3 (1-2 sin²⁡t )=√3 [1-2(y/2)² ]=√3-√3/2 y²，

代入(1)问所求l的直角坐标方程得3y²-2y-4m-6=0，即3y²-2y-6=4m,

由-2≤y≤2，可解得-19/12≤m≤5/2.

故m的范围是-19/12≤m≤5/2.

在直角坐标系xOy中，⨀C的圆心为C(2,1)，半径为1.

(1)写出⨀C的一个参数方程；

(2)过点F(4,1)作⨀C的两条切线，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求这两条切线的极坐标方程.

(1)依题意，⨀C的普通方程为(x-2)²+(y-1)²=1,

所以⨀C的参数方程为,( θ为参数)

(2)由题意，切线的斜率一定存在，设切线方程为y-1=k(x-4)，即kx-y+1-4k=0,

由圆心到直线的距离等于1可得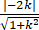=1,解得k=±/3.

∴切线方程为x-3y+3-4=0或x+3y-3-4=0,

代入x=ρcosθ,y=ρsinθ化简得：

2ρ cos⁡(θ+π/3)=4-或2ρ cos⁡(θ-π/3)=4+.