解不等式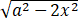
>x+a,(a>0)并就图说明之.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
过一定点作一直线 AB 平行于一定平面 P，且与另一定平面 Q 所成之角等于定角 θ.
于任意 △ABC 之各边上向外作等边三角形 BCD，CAE 及 ABF，试证此诸等边三角形的外接圆共点.若此点为 P，则 PA+PB + PC =AD =BE =CF.
设二曲线c1及c2的方程依次为x²+2xy-3y²+2x+2y+2=0及x²+y²-4=0，求1) 过 c1 及 c2的交点的抛物线；2) 过 c1 及 c2 的交点的二次曲线之心之轨迹.
设 F 是抛物线的焦点，在抛物线上任取一点 P 与焦点连接，由 P 作 PQ平于主轴，试证 P 点的法线平分 ∠FPQ.
设 A,B 为 x 的两个有理整式，请用辗转相除法说明并证明何种情况为互质，何种情况下有公因式.有公因式时，说明求最高公因式之方法并证明之.
分解(x2-2x+5)/(x4-4x3+5x2-4x+4)为最简部分分式.
若a>b>1,p=,Q=(lga+lgb),R=lg((a+b)/2),则【 】
已知函数f(x)=(x2+2x+a)/x,x∈[1,+∞).若对任意x∈[1,+∞),f(x)>0恒成立，试求实数a的取值范围.
已知i,m,n是正整数，且1<i≤m<n.（Ⅰ）证明 niAim<miAin；（Ⅱ）证明 (1+m)n>(1+n)m.
正实数x,y,z,w满足x≥y≥w，且x+y≤2(w+z)，求 + 的最小值.
已知x,y,z>0，判断s=x/(x+y) + y/(y+z) + z/(z+x) 是否存在最大值与最小值.
已知 a > 0, b > 0, 且 a + b = 1, 则【 】
已知函数 f(x) = 2x − x − 1, 则不等式 f(x) > 0 的解集是【 】
已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.