正实数x,y,z,w满足x≥y≥w,且x+y≤2(w+z),求 +
+  的最小值.
的最小值.
问答题(2020年北京大学)
答案解析
 +
+  ≥
≥  +
+ 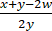 =
=  +
+  +
+ 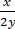 -
-  ≥
≥  +
+ 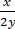 – w•
– w•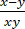
≥  +
+ 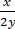 – y•
– y•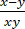 =
=  +
+ 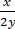 –
– 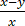 = -
= - +
+ 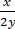 +
+  ≥
≥ -
- 
等号在x= y,y=w,z=
y,y=w,z= (x+y-2w)时成立.
(x+y-2w)时成立.
正实数x,y,z,w满足x≥y≥w,且x+y≤2(w+z),求 +
+  的最小值.
的最小值.
 +
+  ≥
≥  +
+ 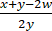 =
=  +
+  +
+ 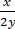 -
-  ≥
≥  +
+ 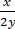 – w•
– w•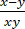
≥  +
+ 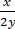 – y•
– y•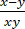 =
=  +
+ 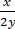 –
– 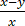 = -
= - +
+ 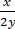 +
+  ≥
≥ -
- 
等号在x= y,y=w,z=
y,y=w,z= (x+y-2w)时成立.
(x+y-2w)时成立.