对任意实数x1,…,xn,证明下述不等式成立:
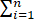
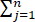
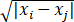 ≤
≤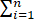
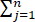
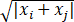 .
.
对任意实数x1,…,xn,证明下述不等式成立:
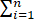
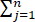
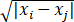 ≤
≤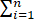
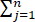
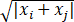 .
.
当n=0时显示成立.当n=1时,原式即0≤,显然亦成立.下设n≥2,需要注意的是,不等式左侧具有平移不变性;即当所有的xi同时加上一个实数λ时,不等式左侧是不变的.我们考察|xi+xj |>0的情形.当2|λ|<|xi+xj |时,不等式右侧可视为一个关于λ的函数f(λ)=+.当2|λ|<|xi+xj |时,该函数关于λ单调递减.当f' (0)≥0时,对λ≤0,有f' (λ)≥f' (0)≥0;当f' (0)...
查看完整答案关于实数x的不等式|x - (a+1)2/2| ≤ (a+1)2/2 与 x2 - 3(a+1)x + 2(3a+1)≤0(a∈R)的解集依次记为A和B,求使A⊆B的a的取值范围.
f(x) =| x − a2 |+ |x − 2a + 1| .(1) 当 a = 2 时, 求不等式 f(x) ⩾ 4 的解集.(2) f(x) ⩾ 4, 求 a 的取值范围.
已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.
已知函数f(x)=|x-a|+|x+3|.(1)当a=1时,求不等式f(x)≥6的解集;(2)若f(x)>-a,求a的取值范围.