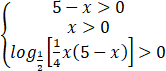高中数学-高考试题(全国统考 1993年基本不等式)

计算题（1993年全国统考）

解不等式2 + (5-x) + log₂(1/x) > 0.

答案解析

原不等式等价于

解得

所以原不等式的解集为{x│0<x<1}∪{x|4<x<5}.

讨论

基本不等式

已知函数 f(x) = 2x − x − 1, 则不等式 f(x) > 0 的解集是【】

已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.

不等式(2-x)/(x+4)>0的解集是__________.

若正数a,b满足ab=a+b+3，则ab的取值范围是__________.

不等式(x-1)/(x-3)>0的解集为【】

已知n为自然数，实数a>1，解关于x的不等式logax - 4loga2x + 12loga3x + ⋯ + n(-2)n-1loganx > (1-(-2)n)/3·loga(x2 - a).

对任意x，y，x2+y2-xy=1，则【】

若实数a,b满足a>b>0，下列不等式中恒成立的是【】

解不等式>x+a,(a>0)并就图说明之.

正实数x,y,z,w满足x≥y≥w，且x+y≤2(w+z)，求 + 的最小值.

对数函数

设 alog34 = 2, 则 4−a =【】

Logistic 模型是常用数学模型之一, 可应用于流行病学领域. 有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 I(t) (t 的单位: 天) 的 Logistic 模型: I(t) = , 其中 K 为最大确诊病例数. 当 I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【】

基本再生数 R0 与世代间隔 T 是新冠肺炎的流行病学基本参数. 基本再生数指一个感染者传染的平均人数, 世代间隔指相邻两代间传染所需的平均时间. 在新冠肺炎疫情初始阶段, 可以用指数模型: I(t) = ert 描述累计感染病例数 I(t) 随时间 t (单位: 天) 的变化规律, 指数增长率 r 与 R0, T 近似满足 R0 = 1 + rT. 有学者基于已有数据估计出 R0 = 3.28, T = 6. 据此, 在新冠肺炎疫情初始阶段, 累计感染病例数增加 1 倍需要的时间约为(ln 2 ≈ 0.69)【】

已知log189=a(a≠2)，18b=5，求log3645.

证明对数换底公式：logbN=logaN/logab.(a,b,N都是正数，a≠1,b≠1)

函数y=10lgx中，x的取值范围是__________.

已知a,b为实数，并且e<a<b，其中e是自然对数的底，证明 ab>ba.

设c,d,x为实数，c≠0,x为未知数.讨论方程 = -1在什么情况下有解.有解时求出它的解.

设对所有实数x，不等式x2log2 4(a+1)/a+2xlog2 2a/(a+1)+log2 (a+1)2/(4a2)>0恒成立，求a的取值范围.

若定义在区间(-1,0)内的函数f(x)=log2a⁡(x+1)满足f(x)>0,则a的取值范围是【】

不等式

若 x, y 满足约束条件则 z = x + 7y 的最大值为 __________.

若 x, y 满足约束条件 , 则 z = x + 2y 的最大值是__________.

若 x, y 满足约束条件, 则 z = 3x + 2y 的最大值是__________.

设a²+b²+c²=1,x²+y²+z²=1，证ax+by+cz≤1.

有一叠n>1 张卡片．在每张卡片上写有一个正整数．这叠卡片具有如下性质：其中任意两张上的数的算术平均值也等于这叠卡片中某一张或几张卡片上的数的几何平均值．确定所有的n，使得可以推出所有卡片上的数均相等．(爱沙尼亚供题)

设 a, b, c ∈ R, a + b + c = 0, abc = 1.(1) 证明: ab + bc + ca < 0;(2) 用 max{a, b, c} 表示 a, b, c 的最大值, 证明: max{a, b, c} ⩾.

The real numbers a,b,c,d are such that a≥b≥c≥d>0 and a+b+c+d=1.Prove that (a+2b+3c+4d)aabbccdd<1.设实数a、b、c、d满足 a≥b≥c≥d>0 ，且 a+b+c+d=1 . 证明：(a+2b+3c+4d)aabbccdd<1.(比利时供题)

关于实数x的不等式|x - (a+1)2/2| ≤ (a+1)2/2 与 x2 - 3(a+1)x + 2(3a+1)≤0(a∈R)的解集依次记为A和B，求使A⊆B的a的取值范围.

已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.

f(x) =| x − a2 |+ |x − 2a + 1| .(1) 当 a = 2 时, 求不等式 f(x) ⩾ 4 的解集.(2) f(x) ⩾ 4, 求 a 的取值范围.