Logistic 模型是常用数学模型之一, 可应用于流行病学领域. 有学者根据公布数据建立了某地区新冠肺炎
累计确诊病例数 I(t) (t 的单位: 天) 的 Logistic 模型: I(t) =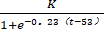 , 其中 K 为最大确诊病例数. 当
I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【 】
, 其中 K 为最大确诊病例数. 当
I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【 】
A、60
B、63
C、66
D、69
Logistic 模型是常用数学模型之一, 可应用于流行病学领域. 有学者根据公布数据建立了某地区新冠肺炎
累计确诊病例数 I(t) (t 的单位: 天) 的 Logistic 模型: I(t) =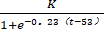 , 其中 K 为最大确诊病例数. 当
I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【 】
, 其中 K 为最大确诊病例数. 当
I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【 】
A、60
B、63
C、66
D、69
C
某地现有耕地10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?
设a∈R,函数f(x)=,若f(x)在区间(0,+∞)内恰好有6个零点,则a的取值范围是【 】
方程(x2006+1)(1+x2+x4+⋯+x2004 )=2006x2005的实数解的个数为__________.
解1/(1+2x)-2/(2+3x)+3/(3+3x)-4/(4+4x)=0.
有甲、乙二书记,甲每写3页.乙能写4页,甲日写8点钟,10日之间已写 480页.问乙欲 15 日之力写完 720 页,每日须写几点钟.
试解方程式(x+2)/(x-2)-(x-2)/(x+2)=5/6.