高中数学-高考试题(南京大学 1933年对数函数)

计算题（1933年南京大学）

log₁₀(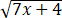+25)-log₁₀⁡x=1

答案解析

暂无答案

讨论

基本初等函数

安徽省基本初等函数

已知a>0且a≠1，函数f(x)=xa/ax (x>0).(1)当a=2时，求f(x)的单调区间；(2)若曲线y=f(x)与直线y=1有且仅有两个交点，求a的取值范围.

化简下式：(1 - c2)-1/2 - {[(1+c)(1-c)]1/2+c2[(1+c)(1-c)]-1/2}.

已知a>0,a≠1，试求使方程loga(x-ak)=(x2-a2)有解的k的取值范围.

已知log5(x2+2x-2) = 0 , 2log5(x+2) - log5y + 1/2 = 0，求y的值.

log89/log23 的值是【】

若loga2<logb2<0，则【】

已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是【】

若定义在区间(-1,0)内的函数f(x)=log2a⁡(x+1))满足f(x)>0,则a的取值范围是【】

若定义在区间(-1,0)内的函数f(x)=log2a⁡(x+1)满足f(x)>0,则a的取值范围是【】

对数函数

青少年视力是社会普遍关注的问题，视力情况可借助视力表测量，通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录法的数据V满足L=5+lgV，已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为(≈1.259)【】

设a=2ln1.01,b=ln1.02,c=-1，则【】

(2lg2+lg3)/(2+lg0.36+2/3 lg8)

河北省对数函数

求(lg3+lg2)/(1/4 lg16++1/2 lg0.09)的值.(其中lg表示以10为底的对数)

计算(2log4⁡3+log8⁡3)(log3⁡2+log9⁡2)的值为【】

求满足方程log2⁡(3x+2)=2+log2(x-2)的x值.

设 alog34 = 2, 则 4−a =【】

Logistic 模型是常用数学模型之一, 可应用于流行病学领域. 有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 I(t) (t 的单位: 天) 的 Logistic 模型: I(t) = , 其中 K 为最大确诊病例数. 当 I(t∗) = 0.95K 时, 标志已初步遏制疫情, 则 t∗ 约为 (ln19 ≈ 3)【】

基本再生数 R0 与世代间隔 T 是新冠肺炎的流行病学基本参数. 基本再生数指一个感染者传染的平均人数, 世代间隔指相邻两代间传染所需的平均时间. 在新冠肺炎疫情初始阶段, 可以用指数模型: I(t) = ert 描述累计感染病例数 I(t) 随时间 t (单位: 天) 的变化规律, 指数增长率 r 与 R0, T 近似满足 R0 = 1 + rT. 有学者基于已有数据估计出 R0 = 3.28, T = 6. 据此, 在新冠肺炎疫情初始阶段, 累计感染病例数增加 1 倍需要的时间约为(ln 2 ≈ 0.69)【】

函数

有甲、乙两人，甲所有银为乙之五倍，其后甲得30元，乙得80元，则甲所有为乙之二倍，问甲、乙原各有银几何?

由甲地至乙地，若每时行 32 丈，则比预定时间迟2小时可到，若每小时行 56 丈，则比预定时间早1小时可到，问依预定时间每时应行之速?

北京工业大学映射与函数

农夫四名，每日工作14小时，5日间可耕田15亩，问用农夫七名，每日工作 13小时，几日可耕田39/2亩?

我国邮政贮金，规定常年4厘2毫.于六月、十二月底结算，可以利息加入本金，但不满一元者不计，今有人以500元于六月底存入，由七月一号起算利息，问三年后可得本利共若干元?

求由1至于某数间之素数之法，并举例以说明之.

A motion picture film 120 feet long contains a certain number of individual pictures.If each picture were 0.1 of an inch shorter, the same film would contain 720 more pictures, how long is each picture?

Draw the graph of the equation (1) y = x³ - x² - x + 1.Use the graph to locate the roots of the equation (2) x³ - x² - x + 1 = 0.Check by solving the equation algebraically.

一坐自行车者以平均速度行过 180 哩，设彼每小时迟行三哩，则行此路程须多加三小时，问其速度若何?

已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.