高中数学-高考试题(全国统考 1989年数列与推理)

问答题（1989年全国统考）

是否存在常数a,b,c使得等式1∙2²+2∙3²+⋯+n∙(n+1)₂=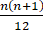(an²+bn+c)对一切自然数n都成立？并证明你的结论.

答案解析

因为n∙(n+1)2=n3+2n2+n，所以Sn=1∙22+2∙32+⋯+n∙(n+1)2=(13+2∙12+1)+(23+2∙22+2)+⋯+(n3+2n2+n)=(13+23+⋯+n3)+2(12+22+⋯+n2)+(1+2+⋯+n)由于下列等式对一切...

查看完整答案

讨论

高中数学

已知a>0,a≠1，试求使方程loga(x-ak)=(x2-a2)有解的k的取值范围.

自点A(-3,3)发出的光线l射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线l所在直线的方程.

如图，在平行六面体ABCD-A1B1C1D1中，已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=π/3. (Ⅰ)求证：顶点A1在底面ABCD的射影O在∠BAD的平分线上；(Ⅱ)求这个平行六面体的体积.

证明：tan 3x/2 - tan x/2=2sinx/(cosx+cos2x) .

如图，已知圆柱的底面半径是3，高是4，A，B两点分别在两底面的圆周上，并且AB=5，那么直线AB与轴oo'之间的距离等于______.

已知A和B是两个命题，如果A是B的充分条件，那么B是A的______条件；A ̅是B ̅的______条件.

已知(1-2x)7=a0+a1 x+a2 x2+⋯+a7 x7，那么a1 x+a2+⋯+a7=__________.

函数y=(ex-1)/(ex+1)的反函数的定义域是__________.

不等式|x2-3x|>4的解集是____________.

方程sinx-cosx=的解集是____________________.

数列

设正数数列{an },{bn}满足：a1=b1=1,bn=an bn-1-1/4(n≥2).求4+1/(a1 a2⋯ak )的最小值，其中m是给定的正整数.

Find the sum of n terms of the series whose nth term is 3(4n+4n²)-5n³.

Find the general term and the sum ofn terms of the series -3,-1,11,39,89,167.

Find the sum of the geometical series -2,,-1/3 to 6 terms.

求证 1³+2³+3³+⋯+n³=[n(n+1)/2]²

求级数1/(1×3)+1/(3×5)+1/(5×7)+⋯ n项及无穷项之和.其第n项为1/(2n-1)(2n+1).

若a1,a2,⋯,an为已知正数，试求atctan(a1-a2)/(1+a1 a2)+atctan(a2-a3)/(1+a2 a3)+⋯+atctan(an-1-an)/(1+an-1 an)的值.

级数1!/102 -2!/103 +3!/104 -⋯是收敛的还是发散的？

已知一级数第n项为lg⁡，试求此级数前几项之和.

已知数列{an}满足an+1=1/4 (an-6)³+6(n=1,2,3,⋯)，则【】

数列与推理

已知数列{an },{bn}的项数均为m(m>2)，且an,bn∈{1,2,⋯,m},{an },{bn}的前n项和分别为An,Bn，并规定A0=B0=0.对于k∈{0,1,2,⋯,m}，定义rk=max⁡{i|Bi≤Ai,i∈{0,1,2,⋯,m}}，其中maxM表示数集M中最大的数.(1)若a1=2,a2=1,a3=3,b1=1,b2=3,b3=3，求r0,r1,r2,r3的值；(2)若a1≥b1,2rj≤rj+1+rj-1,j=1,2,⋯,m-1，求rn；(3)证明：存在p,q,s,t∈{0,1,2,⋯,m}，满足p>q,s>t，使得Ap+Bt=Aq+Bs.

令S=m²n/(2m(n2m+m2n))，则[100S]=________.

给定整数k≥2.求所有无穷正整数数列a1,a2,⋯,使得存在多项式P(x)=xk+ck-1 xk-1+⋯+c1 x+c0其中c0,c1,⋯,ck-1是非负整数，满足P(an )=an+1 an+2⋯an+k对任意正整数n成立.

已知数列{an}满足：a1=1，a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*)，求a2020的个位数.

数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.

数列 {an} 中, a1 = 2, am+n = aman , 若 ak+1 + ak+2 + · · · + ak+10 = 215 − 25, 则 k=【】

0−1 周期序列在通信技术中有着重要应用. 序列 a1a2 · · · an · · · 满足 a1 ∈ {0, 1} (i = 1, 2, · · · ), 且存在正整数 m, 使得 ai+m = ai (i = 1, 2, · · · ) 成立, 则称其为 0−1 周期数列, 并称满足 ai+m = ai (i = 1, 2, · · · ) 的最小正整数 m 为这个序列的周期. 对于周期为 m 的 0−1 序列 a1a2 · · · an · · · , C(k) =(k = 1, 2, · · · , m−1)是描述其性质的重要指标. 下列周期为 5 的 0 − 1 序列中, 满足 C(k) ⩽ 1/5(k = 1, 2, 3, 4) 的序列是【】

如图, 将钢琴上的 12 个键依次记为 a1, a2, · · · , a12, 设 1 ⩽ i ⩽ j ⩽ k ⩽ 12. 若 k − j = 3 且 j − i = 4, 则称 ai, aj, ak 为原位大三和弦; 若 k − j = 4 且 j − i = 3, 则称 ai, aj, ak 为原位小三和弦. 用这 12 个键可以构成的原位大三和弦与原位小三和弦的个数之和为【】

设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.

信息熵是信息论中的一个重要概念. 设随机变量 X 所有可能的取值为 1, 2, … , n, 且 P (X = i) = pi >0 (i = 1, 2, …, n), =1, 定义 X 的信息熵 H(X) = −log2 pi.【】