等差数列{an}的各项均为正数，首项与公差相等，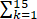
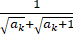=2，则a4的值为【 】
A、6
B、7
C、8
D、9
E、10
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知函数f(x)=2x3-9x2+ax+5在x=1处取得极大值，在x=b处取得极小值，则a+b的值为【 】
已知tanθ<0,cos(π/2+θ)=√5/5，则cosθ的值为【 】
设f(x)为多项式函数，g(x)=x2 f(x)，若f(2)=1,f'(2)=3，则g'(2)的值为【 】
在公比为正数的等比数列{an}中，a2+a4=30,a4+a6=15/2，则a1的值为【 】
设正多面体每个顶点连有M条棱，每面都是正N边形，则正整数M和N满足关系：M>2，N>2，MN<2(M+N)，这种正多面体共有【 】种。
记 Sn 为等差数列 {an} 的前 n 项和, 若 a1 = −2, a2 + a6 = 2, 则 S10 = ______.
在等差数列 {an} 中, a1 = −9, a5 = −1. 记 Tn = a1a2 · · · an (n = 1, 2, · · · ), 则数列 {Tn}【 】
已知数列 {an} 为不为零的等差数列, 且 a1 + a10 = a9, 则 (a1+a2+⋯+a9)/a10 =__________ .
已知等差数列 {an} 的前 n 项和为 Sn, 公差 d≠ 0, a1/d ⩽ 1. 记 b1 = S2, bn+1 = Sn+2 − S2n, n ∈ N∗, 下列不可能成立的是【 】
我国古代数学家杨辉、宋世杰等研究过高阶等差数列求和问题, 如数列 {n(n+1)/2} 就是二阶等差数列,数列{n(n+1)/2} (n ∈ N∗) 的前 3 项和是________.
若(z-x)2-4(x-y)(y-z)=0，求证：x,y,z成等差数列.
设等差数列{an}的前n项和为Sn.已知a3=12,S12>0,S13<0.(Ⅰ)求公差d的取值范围.(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.
等比数列{an}的首项a1=-1，前n项和为Sn，若S10/S5 =31/32,则Sn 等于【 】
已知数列{an }，{bn }都是由正数组成的等比数列，公比分别为p,q，其中p>q且p≠1,q≠1，设cn= an+bn，Sn为数列{cn}的前n项和.求Sn/Sn-1 .
在等比数列{an}中，a1>1，且前n项和Sn满足Sn=1/a1 ，那么a1的取值范围是【 】
已知数列{cn},其中cn=2n+3n,且数列{cn+1 - pcn}为等比数列，求常数p.
设{cn}，{bn}是公比不相等的两个比数列，cn =an+bn.证明数列{cn}不是等比数列.