高中数学-高考试题(全国统考 1982年数列与推理)

问答题（1982年全国统考）

已知数列a₁,a₂,⋯a_n,⋯和数列b₁,b₂,⋯b_n,⋯，其中a₁=p,b₁=q,a_n=pa_n-1,b_n=qa_n-1+rb_n-1 (n≥2)（p,q,r是已知常数，且q≠0,p>r>0）.

(1) 用p,q,r,n表示b_n，并用数学归纳法加以证明；

(2) 求.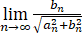

答案解析

(1)∵a1=p,an=pan-1,∴an=pn.又b1=q,b2=qa1+rb1=q(p+r),b_3=qa2+rb2=q(p2+pr+r2), …设想bn=q(pn-1+pn-2 r+⋯+rn-1 )=.用数学归纳法证明：当n=2时，b2=q(p+r)=，等式成立；...

查看完整答案

讨论

高中数学

抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切，证明这个三角形的第三边也与抛物线x2=2qy相切.

已知空间四边形ABCD中AB=BC,CD=DA,M,N,P,Q分别是边AB,BC,CD,DA的中点（如图）.求证MNPQ是一个矩形.

如图：已知锐角∠AOB=2α内有动点P，PM⊥OA，PN⊥OB，且四边形PMON的面积等于常数c2.今以∠AOB的角平分线OX为极轴，求动点P的轨迹的极坐标方程，并说明它表示什么曲线.

设0<x<1,a>0,a≠1，比较|loga(1-x)|与|loga(1+x)|的大小（要写出比较过程）.

已知圆锥体的底面半径为R，高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).

在平面直角坐标系内，下述方程表示什么曲线？画出它的图形.

在平面直角坐标系内，下述方程表示什么曲线？画出它的图形.

求y=cos2 的导数.

求(-1+i)20展开式中第15项的数值.

函数y=lg10x中，x的取值范围是__________.

数列

嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{bn}：b1=1+ ，b2=1+，b3=1+，…，依此类推，其中αk∈N* (k=1,2,⋯)．则【】

己知数列{an}各项均为正数，其前n项和Sn满足an⋅Sn=9(n=1,2,⋯)．给出下列四个结论：①{an}的第2项小于3； ②{an}为等比数列；③{an}为递减数列； ④{an}中存在小于1/100的项．其中所有正确结论的序号是__________．

已知Q:a1,a2,⋯,ak为有穷整数数列．给定正整数m，若对任意的n∈{1,2,⋯,m}，在Q中存在ai,ai+1,ai+2,⋯,ai+j (j≥0)，使得ai+ai+1+ai+2+⋯+ai+j=n，则称Q为m-连续可表数列．（1）判断Q:2,1,4是否为5-连续可表数列？是否为6-连续可表数列？说明理由；（2）若Q:a1,a2,⋯,ak为8-连续可表数列，求证：k的最小值为4；（3）若Q:a1,a2,⋯,ak为20-连续可表数列，且a1+a2+⋯+ak<20，求证：k≥7．

已知数列{an}满足a1=1,an+1=an-1/3 an2 (n∈N* )，则【】

(I)设{an}是集合{2t+2s |0≤s<t,s,t∈Z}中所有的数从小到大排列成的数列，即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,⋯将数列{an}各项按照上小下大，左小右大的原则写成如下的三角形数表:35 69 10 12⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯⋯(i)写出这个三角形数表的第四行、第五行各数;(ii)求a100.(Ⅱ)(本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分)设{bn}是集合{2t+2s+2r |0≤r<s<t,r,s,t∈Z}中所有的数从小到大排列成的数列，已知bk=1160，求k.

设正数数列{an}满足：a1=1+√2且(an-an+1 )(an+an-1-2√n)=2(n≥2).(1)求数列{an}的通项公式；(2)求满足[an ]=2022的所有正整数n构成的集合([x]表示不超过x的最大整数).

设正数数列{an },{bn}满足：a1=b1=1,bn=an bn-1-1/4(n≥2).求4+1/(a1 a2⋯ak )的最小值，其中m是给定的正整数.

在各项均为正数，且满足下列条件的数列{an}中，a9可能的最大值和最小值分别为M和m，则M+m的值为【】(1) a7=40(2)对于任意正整数n，an+2=

数列{an },{bn}满足(3ak+5)=55,(ak+bk)=32，求bk 的值.

有半径为R之圆C，于其直径AB上取其半B1 B为直径作一圆C1，又取B1 B之半B2 B为直径作一圆C2，更取B2 B之半B3 B为直径作一圆C3，如是无限推之，求C1,C2,C3,⋯无穷个圆周之和.

数列与推理

Find the sum of n terms of the series whose nth term is 3(4n+4n²)-5n³.

Find the general term and the sum ofn terms of the series -3,-1,11,39,89,167.

Find the sum of the geometical series -2,,-1/3 to 6 terms.

求证 1³+2³+3³+⋯+n³=[n(n+1)/2]²

求级数1/(1×3)+1/(3×5)+1/(5×7)+⋯ n项及无穷项之和.其第n项为1/(2n-1)(2n+1).

有相交之二直线 a 及 b，自 a 上之一点作 b 之垂线，复自其在 b 上之垂足向 a作垂线，更自第二个垂足作 b 之垂线，如此继续作成无数根垂线，设第一垂线之长为 7，第二垂线之长为 6，求此无数垂线长之和.

设a,b,c三数成调和级数，试证1/a+1/c+1/(a-b)+1/(c-b)=0.

已知一级数第n项为lg⁡，试求此级数前几项之和.

已知数列{an}满足an+1=1/4 (an-6)³+6(n=1,2,3,⋯)，则【】

已知数列{an },{bn}的项数均为m(m>2)，且an,bn∈{1,2,⋯,m},{an },{bn}的前n项和分别为An,Bn，并规定A0=B0=0.对于k∈{0,1,2,⋯,m}，定义rk=max⁡{i|Bi≤Ai,i∈{0,1,2,⋯,m}}，其中maxM表示数集M中最大的数.(1)若a1=2,a2=1,a3=3,b1=1,b2=3,b3=3，求r0,r1,r2,r3的值；(2)若a1≥b1,2rj≤rj+1+rj-1,j=1,2,⋯,m-1，求rn；(3)证明：存在p,q,s,t∈{0,1,2,⋯,m}，满足p>q,s>t，使得Ap+Bt=Aq+Bs.