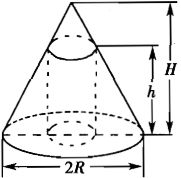
已知圆锥体的底面半径为R，高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知圆锥的顶点为P，底面圆心为O,AB为底面直径，∠APB=120°,AP=2，点C在底面圆周上，且二面角P-AC-O为45°，则【 】
已知圆锥面x²+y²=z²/3，记沿该圆锥面从P(-√3,3,6)到Q(√3,0,3)的曲线长度的最小值为I，则[10I]=________.
已知圆柱和圆锥的底面半径相等，侧面积相等，且它们的高均为√3，则圆锥的体积为【 】
设圆锥底面圆周上两点A,B间的距离为2,圆锥顶点到直线AB的距离为,AB和圆锥的轴的距离为1,则该圆锥的体积为________.
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是________.
若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的全面积是【 】
对24小时内降水在平地上的积水厚度(mm)进行如下定义：小雨：0~10中雨：10~25大雨：25~50暴雨：50~100小明用一个圆锥形容器接了24小时的雨水，则这一天的雨水属于哪个等级【 】
两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为32π/3，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为【 】
如图，四边形ABCD为正方形， ED⊥平面ABCD，FB//ED,AB=ED=2FB，记三棱锥E-ACD,F-ABC，F-ACE的体积分别为V1,V2,V3，则【 】
设一四面体有一三面角与另一四面体的一三面角对称，求证：其体积之比等于此两三面角三棱分别的乘积之比.
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
已知三棱锥D-ABC的三个侧面与底面全等，且AB=AC=,BC=2，则以BC为棱，以面BCD与面BCA为面的二面角的大小是【 】
一个长方体共一顶点的三个面的面积分别是,, ,这个长方体对角线的长是【 】
在正三棱锥ABC-A1B1C1中，若AB=BB1，则AB1与C1B所成的角的大小为【 】
已知A,B,C是半径为1的球O的球面上的三个点，且AC⊥BC,AC=BC=1，则三棱锥O-ABC的体积为【 】
如图，长方体ABCD-A1 B1 C1 D1中，已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点，求三棱锥C-PAD的体积；(2)求直线AB1与平面ACC1 A1的夹角大小.