如图是函数 y = sin(ωx +φ) 的部分图像, 则 sin(ωx +φ) =【 】
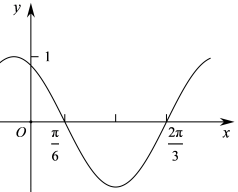
A、sin(x + π/3)
B、sin(2π/3-2x)
C、cos(2x + π/6)
D、cos(5π/6-2x)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
若定义在 R 的奇函数 f(x) 在 (−∞, 0) 单调递减, 且 f(2) = 0, 则满足 xf(x − 1) ⩾ 0 的 x 的取值范围是【 】
已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则• 的取值范围是【 】
某中学的学生积极参加体育锻炼, 其中有 96% 的学生喜欢足球或游泳, 60% 的学生喜欢足球, 82% 的学生喜欢游泳, 则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是【 】
6 名同学到甲、乙、丙三个场馆做志愿者, 每名同学只去 1 个场馆, 甲场馆安排 1 名, 乙场馆安排 2 名, 丙场馆安排 3 名, 则不同的安排方法共有【 】
设函数f(x)=sinx+cosx(x∈R).(1)求函数y=[f(x+π/2)]2的最小正周期;(2)求函数y=f(x)f(x-π/4)在[0,π/2]上的最大值.
求证：(sinα+sinβ)/sin(α+β)=cos((α-β)/2)/cos((α+β)/2)
计算：sin 4π/3∙cos 25π/6∙tg(-3π/4).
证明：(sin2α+1)/(1+cos2α+sin2α)=1/2 tanα+1/2.
已知x+x-1=2cosθ，求证：xn+x-n=2cosnθ.
记△ABC的内角A，B，C的对边分别为a，b，c，已知cosA/(1+sinA )=(sin2B)/(1+cos2B)．（1）若C=2π/3，求B；（2）求(a2+b2)/c2 的最小值．
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
已知函数 f(x) = sinx + 1/sinx, 则【 】
函数y=tan(1/2 x - 1/3 π)在一个周期内的图像是【 】
已知函数f(x)=2cos(ωx+φ)的部分图像如图所示，则满足条件(f(x)-f(-7π/4))(f(x)-f(4π/3))>0的最小正整数x为______.
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍，纵坐标不变，再把所得曲线向右平移π/3个单位长度，得到函数sin(x-π/4)的图像，则f(x)=【 】
记函数f(x)=sin(ωx+π/4)+b(ω>0)的最小正周期为T.若2/3 π<T<π，且y=f(x)的函数图像关于点(3π/2,2)中心对称，则f(π/2)=【 】
函数f(x)=sin(2x+φ)(0<φ<π)的图像以(2π/3,0)中心对称，则【 】
将函数f(x)=sin(ωx+π/3) (ω>0)的图像向左平移π/2个单位长度后得到曲线C，若C关于y轴对称，则ω的最小值是【 】