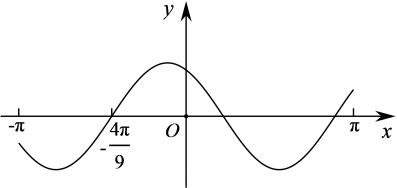
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
A、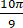
B、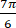
C、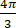
D、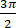
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。

A、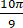
B、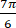
C、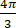
D、
C由图知 = 0, 所以 = + kπ (k ∈ Z), 化简得ω=-(k ∈ Z).又因为 T < 2π < 2T, 即 < 2π <, 所以 1 < |ω| &...
查看完整答案函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【 】。
已知 A 为抛物线 C : y2 = 2px(p > 0) 上一点, 点 A 到 C 的焦点的距离为 12, 到 y 轴的距离为 9, 则 p=【 】。
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
设集合 A ={x | x2 −4 ⩽ 0},B ={x | 2x + a ⩽ 0}, 且 A∩B ={x |−2 ⩽ x ⩽ 1}, 则 a =【】
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
Prove that:tan-11/3+tan-11/5+tan-11/7+tan-11/8=45°
Solve 1+1+2/(1-tan²x )-(3-tan²x)/(1-3 tan²x )=0
Solve secx - cotx = cscx - tanx
求适合sin2x+cos2x=√2 sinx及0≤x≤2π的角的值.
解三角方程 sin³θ + cosθ = sinθ + cos³θ.
若A+B+C=180°,证:sin(B+2C)+sin(C+2A)+sin(A+2B)=4 sin1/2(B-C)∙sin1/2 (C-A)∙sin1/2(A-B)
试证arcsinx+arcsiny=arcsin(x+y).
证明: cos(α+β-γ)+cos(α-β+γ)-cos(β+γ-α)-cos(α+β+γ)=4cosα∙sinβ∙sinγ.
为了得到函数y=2sin3x的图像,只要把函数y=2sin(3x+π/5)图像上所有的点【 】
函数y=tan(1/2 x - 1/3 π)在一个周期内的图像是【 】
已知函数f(x)=2cos(ωx+φ)的部分图像如图所示,则满足条件(f(x)-f(-7π/4))(f(x)-f(4π/3))>0的最小正整数x为______.
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍,纵坐标不变,再把所得曲线向右平移π/3个单位长度,得到函数sin(x-π/4)的图像,则f(x)=【 】
记函数f(x)=sin(ωx+π/4)+b(ω>0)的最小正周期为T.若2/3 π<T<π,且y=f(x)的函数图像关于点(3π/2,2)中心对称,则f(π/2)=【 】
函数f(x)=sin(2x+φ)(0<φ<π)的图像以(2π/3,0)中心对称,则【 】
将函数f(x)=sin(ωx+π/3) (ω>0)的图像向左平移π/2个单位长度后得到曲线C,若C关于y轴对称,则ω的最小值是【 】