已知函数f(x),g(x)的定义域均为R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7.若y=g(x)的图像关于直线x=2对称,g(2)=4,则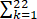 f(k)【 】
f(k)【 】
A、-21
B、-22
C、-23
D、-24
已知函数f(x),g(x)的定义域均为R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7.若y=g(x)的图像关于直线x=2对称,g(2)=4,则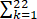 f(k)【 】
f(k)【 】
A、-21
B、-22
C、-23
D、-24
D因为y=g(x)的图像关于直线x=2对称,所以g(2-x)=g(x+2),因为g(x)-f(x-4)=7,所以g(x+2)-f(x-2)=7,即g(x+2)=7+f(x-2),因为f(x)+g(2-x)=5,所以f(x)+g(x+2)=5,代入得f(x)+[7+f(x-2)]=5,即f(x)+f(x-2)=-2,所以f(3)+f(5)+⋯+f(21)=(-2)×5=-10,f(4)+f(6)+⋯+f(22)=(-2)×5=-10.因为f(x)+g(2-x)=5,所以f(0)+g(2)=5,...
查看完整答案在下列各图中,y=ax2+bx与y=ax+b (ab≠0)的图像只能是【 】
给定实数a,a≠0,a≠1,设函数y=(x-1)/(ax-1)(x∈R,x≠1/a).证明:(Ⅰ)经过这个函数图像上任意两个不同的点的直线不平行于x轴;(Ⅱ)这个函数的图像关于直线y=x成轴对称图形.
如图,图中曲线是幂函数y=xn在第一象限的图像.已知n取±2,±1/2四个值则相应于曲线C1,C2,C3,C4的n依次为【 】
设函数f(x) = 1 - (-1≤x≤0),则函数y=f-1(x)的图像是【 】
当a>1时,在同一坐标系中,函数y=a-x与y=logax的图像是【 】
已知f(x)=3/x+2,则f-1 (1)=__________.
若函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)f(y),f(1)=1,则f(k)=【 】
已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.
设函数 f(x) = x3 − 1/x3 , 则 f(x)【 】
对任意不等于1的正数a,函数f(x)=loga( x+3)的反函数的图像都经过点P,则点P的坐标为______.
函数y=(ex-1)/(ex+1)的反函数的定义域是__________.