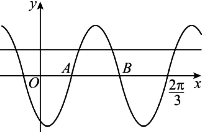
已知函数f(x)=sin(ωx+φ)，如图A,B是直线y=1/2与曲线y=f(x)的两个交点，若|AB|=π/6，则f(π)=________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知直线l:x-my+1=0与⨀C:(x-1)²+y²=4交于A,B两点，写出满足“△ABC的面积为8/5”的m的一个值______.
底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为______.
已知向量a→,b→满足|a→-b→ |=√3,|a→+b→ |=|2a→-b→|，则|b→ |=________.
若函数f(x)=alnx+b/x+c/x² (a≠0)既有极大值也有极小值，则【 】
设O为坐标原点，直线y=-√3(x-1)过抛物线C:y²=2px(p>0)的焦点，且与C交于M,N两点，l为C的准线，则【 】
已知圆锥的顶点为P，底面圆心为O,AB为底面直径，∠APB=120°,AP=2，点C在底面圆周上，且二面角P-AC-O为45°，则【 】
记Sn为等比数列{an}的前n项和，若S4=-5,S6=21S2，则S8=【 】
设x=sinα,且α∈[-π/6,5π/6]，则arccosx的取值范围是________.
若α∈(0,π/2),tan2α=cosα/(2-sinα)，则tanα=【 】
已知函数f(x)=2cos(ωx+φ)的部分图像如图所示，则满足条件(f(x)-f(-7π/4))(f(x)-f(4π/3))>0的最小正整数x为______.
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍，纵坐标不变，再把所得曲线向右平移π/3个单位长度，得到函数sin(x-π/4)的图像，则f(x)=【 】
求证：(sinα+sinβ)/sin(α+β)=cos((α-β)/2)/cos((α+β)/2)
计算：sin 4π/3∙cos 25π/6∙tg(-3π/4).