在120°的二面角P-α-Q的两个面P和Q内,分别有点A和B . 已知点A和点B到棱α的距离分别为2和4,且线段AB=10.
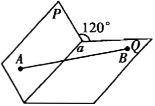
(1) 求直线AB和棱α所成的角;
(2) 求直线AB和平面Q所成的角.
在120°的二面角P-α-Q的两个面P和Q内,分别有点A和B . 已知点A和点B到棱α的距离分别为2和4,且线段AB=10.

(1) 求直线AB和棱α所成的角;
(2) 求直线AB和平面Q所成的角.
(1) 在平面P内作直线AD⊥α于点D;在平面Q内,作直线BE⊥α于点E,在平面Q内作α的垂线与从点B作α的平行线相交于点C.∴ ∠ABC等于AB和α所成的角. ∠ADC为二面角P-α-Q的平面角,∴∠ADC=120°.又AD=2, BCDE为矩形,∴CD=BE=4.连接∴AC,由余弦定理得∴AC2=AD2+CD2-2AD∙CD∙cos120°=4+16-2×2×4×(-1/2) =28 ∴AC=2.又因AD⊥α, CD⊥α,所以α垂直于△ACD所在的平面.再由B...
查看完整答案A:点(a,b)在圆x2+y2=R2上;B:a2+b2=R2,则A是B的__________条件.
A:θ=150°;B:sinθ=1/2,则A是B的__________条件.
A:a=3;B:|a|=3,则A是B的__________条件.
A:四边形ABCD为平行四边形.B:四边形ABCD为矩形.则A是B的________条件.
在 A , B , C , D 四位候选人中:1.如果选举正、副班长各一人,共有几种选法?写出所有可能的选举结果.2.如果选举班委三人,共有几种选法?写出所有可能的选举结果.
设 A 表示有理数的集合, B 表示无理数的集合,即设 A ={有理数} , B ={无理数},试写出:1. A∪B ; 2 . A∩B .
如图所示四面体A-BCD中,AB,BC,BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角大小为arccos /10,求四面体A-BCD的体积.
在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为【 】
如图,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则【 】
下列五个正方体图形中,l是正方体的一条对角线,点 M,N,P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是________(写出所有符合要求的图形序号).
已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体,其中两个面分别位于平面P1和P2上,下面哪条直线可能是该四面体的一条棱【 】
Find the equation of the projection of the linex=z+2,y=2z-4 upon the plane x+y- z = 0.