解不等式(x为未知数):
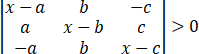
解不等式(x为未知数):
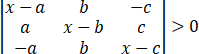
原行列式可逐步简化如下:
∆=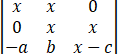 (第二行加到第一行,第三行加到第二行)
(第二行加到第一行,第三行加到第二行)
=x2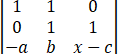
=x2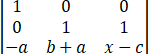 =x2 (x-a-b-c),
=x2 (x-a-b-c),
故原不等式为 x2 (x-a-b-c)>0.
原不等式的解是x≠0,x>a+b+c.
A:点(a,b)在圆x2+y2=R2上;B:a2+b2=R2,则A是B的__________条件.
A:θ=150°;B:sinθ=1/2,则A是B的__________条件.
A:a=3;B:|a|=3,则A是B的__________条件.
A:四边形ABCD为平行四边形.B:四边形ABCD为矩形.则A是B的________条件.
在 A , B , C , D 四位候选人中:1.如果选举正、副班长各一人,共有几种选法?写出所有可能的选举结果.2.如果选举班委三人,共有几种选法?写出所有可能的选举结果.
设 A 表示有理数的集合, B 表示无理数的集合,即设 A ={有理数} , B ={无理数},试写出:1. A∪B ; 2 . A∩B .
设直线(l)的参数方程是 (t是参数)椭圆(E)的参数方程是 (θ是参数)问:a,b应满足什么条件,使得对于任意m值来说,直线(l)与椭圆(E)总有公共点?
若多项式 f(x) 之系数皆为整数,且 f(0) 及 f(1) 又均为奇数,试证 f(x) = 0绝无整数根.
试分解(x²+x-3)/(x-1)(x-2)(x-3)为最简部分分式.
将f(x)=x³-3x²+5x+6的根增一常数 ,使变后的方程缺x²项.
试从x=by+cz,y=cz+ax,z=ax+by,消去x,y,z.求a,b,c间的关系式.
化(5x²-4x+16)/((x²-x+1)²(x-3))为部分分式.
分解(x2-2x+5)/(x4-4x3+5x2-4x+4)为最简部分分式.
设 A,B 为 x 的两个有理整式,请用辗转相除法说明并证明何种情况为互质,何种情况下有公因式.有公因式时,说明求最高公因式之方法并证明之.