有理数加群(Q,+)，记所有分母不超过10的有理数构成的子集为G，其对应的陪集GZ记为G ̅，则Q/Z包含G ̅的最小子群的阶为______.

设20阶实矩阵A满足e^A=I₂₀，且A在复数域上的所有特征值模长均不超过20，则这样的互不相似的A有______个.

令A,B,C,D,E,F是三阶实方阵，且

=.

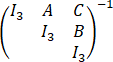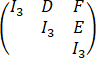已知

A=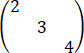,B=

且C=A+B-I，则[|detF|]=______.

A polynomial P with integer coefficients is square-free if it is not expressible in the form P=Q² R, where Q and R are polynomials with integer coefficients and Q is not constant. For a positive integer n, let P_n be the set of polynomials of the form

1+a₁ x+a₂ x²+⋯+a_n xⁿ

with a₁,a₂,⋯,a_n∈{0,1}. Prove that there exists an integer N so that, for all integers n>N, more than 99% of the polynomials in P_n are square-free.

【译】我们称整系数多项式P是无平方因子的，如果其不能表示为P=Q² R的形式，这里Q,R为整系数多项式且Q不为常数.对于正整数n，记P_n为如下 形式的多项式组成的集合：

1+a₁ x+a₂ x²+⋯+a_n xⁿ

这里a₁,a₂,⋯,a_n∈{0,1}.证明：存在整数N，使得对任意的整数n≥N,P_n中超过99%的多项式都是无平方因子的.

复矩阵A与A的任意正整数次常相似.

(1)证明:A的特征值为0或 1;

(2)求A的若当标准型.