高中数学-高考试题(清华大学 2024年矩阵)

填空题（2024年清华大学）

令A,B,C,D,E,F是三阶实方阵，且

=.

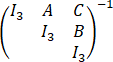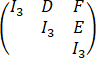已知

A=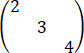,B=

且C=A+B-I，则[|detF|]=______.

答案解析

60

【解析】

解答过程见word版

讨论

高中数学

已知圆锥面x²+y²=z²/3，记沿该圆锥面从P(-√3,3,6)到Q(√3,0,3)的曲线长度的最小值为I，则[10I]=________.

对于一个实数x，令{x}=x-[x]. 记S=min⁡({x/8},{x/4}) dx，则[S]=______.

A polynomial P with integer coefficients is square-free if it is not expressible in the form P=Q² R, where Q and R are polynomials with integer coefficients and Q is not constant. For a positive integer n, let Pn be the set of polynomials of the form1+a1 x+a2 x²+⋯+an xnwith a1,a2,⋯,an∈{0,1}. Prove that there exists an integer N so that, for all integers n>N, more than 99% of the polynomials in Pn are square-free.【译】我们称整系数多项式P是无平方因子的，如果其不能表示为P=Q² R的形式，这里Q,R为整系数多项式且Q不为常数.对于正整数n，记Pn为如下形式的多项式组成的集合：1+a1 x+a2 x²+⋯+an xn这里a1,a2,⋯,an∈{0,1}.证明：存在整数N，使得对任意的整数n≥N,Pn中超过99%的多项式都是无平方因子的.

Let BC be a fixed segment in the plane, and let A be a variable point in the plane not on the line BC. Distinct points X and Y are chosen on the rays (CA) ⃗ and (BA) ⃗, respectively, such that ∠CBX=∠YCB=∠BAC.Assume that the tangents to the circumcircle of ABC at B and C meet line XY at P and Q, respectively, such that the points X,P,Y, and Q are pairwise distinct and lie on the same side of BC. Let Ω1 be the circle through X and Y centred on BC. Similarly let Ω2 be the circle through Y and Q centred on BC. Prove that Ω1 and Ω2 intersect at two fixed points as A varies.【译】在同一平面内，BC为给定线段，动点A不在直线BC上. X和Y分别为射线(CA) ⃗，射线(BA) ⃗上不重合的两点，满足∠CBX=∠YCB=∠BAC.若三角形ABC外接圆在点B和C处的切线分别交直线XY于点P和点Q，点X,P,Y,Q不重合，且位于直线BC同侧.圆Ω1经过点X,P且圆心在BC上.类地，圆Ω2经过点Y,Q且圆心在BC上.证明：当点A运动时，圆Ω1和圆Ω2始终交于两定点.

Fix integers a and b greater than 1. For any positive integer n, let rn be the (non-negative) remainder that bn leaves upon division by an. Assume there exists a positive integer N such that rn<2n/n for all integers n≥N.Prove that a divides b.给定大于1的整数a和b.对任意的正整数n，记rn为bn除以an的非负余数.若存在正整数N，使得对任意的n≥N，都有rn<2n/n.证明：a整除b.

Given a positive integer n, a set S is n-admissible if①each element of S is an unordered triple of integers in {1,2,⋯,n},②|S|=n-2,and③for each 1≤k≤n-2 and each choice of k distinct A1,A2,⋯,Ak∈S,|A1∪A2∪⋯∪Ak |≥k+2Is it true that, for all n>3 and for each n-admissible set S, there exist pairwise distinct points P1,P2,⋯,Pn in the plane such that the angles of the triangle Pi Pj Pk are all less than 61° for any triple {i,j,k} in S?【译】给定正整数n，称集合S是n-可行,如果其满足以下条件：①S的每个元素都是{1,2,⋯,n}的三元子集；②|S|=n-2；③对任意的1≤k≤n-2和任意k个互不相同的A1,A2,⋯,Ak∈S，都有|A1∪A2∪⋯∪Ak |≥k+2判断以下命题是否为真：对所有n>3和所有的n-可行集合S，在平面内总存在n个互不相同的点P1,P2,⋯,Pn，使得对集合S中任意元素{i,j,k}，三角形Pi Pj Pk的每个内角都小于61°.

Consider an odd prime p and a positive integer N<50p. Let a1,a2,⋯,aN be a list of positive integers less than p such that any specific value occurs at most 51/100 N times and a1,a2,⋯,aN is not divisible by p. Prove that there exists a permutation b1,b2,⋯,bN of the a_i such that, for all k=1,2,⋯,N, the sum b1+b2+⋯+bk is not divisible by p.【译】已知奇素数p和正整数N<50p.设a1,a2,⋯,aN是一些小于p的正整数，同一数值至多出现51/100 N次，且a1+a2+⋯+aN不能被p整除.证明：存在a_i的一个排列：b1,b2,⋯,bN，使得对任意的k=1,2,⋯,N，都有b1+b2+⋯+bk不能被p整除.

Let n be a positive integer. Initially, a bishop is placed in each square of the top row of a 2n×2n chessboard; those bishops are numbered from 1 to 2n ,from left to right. A jump is a simultaneous move made by all bishops such that the following conditions are satisfied:each bishop moves diagonally, in a straight line, some number of squares, andat the end of the jump, the bishops all stand in different squares of the same row.Find the total number of permutations σ of the numbers 1,2,⋯,2n with the following property: There exists a sequence of jumps such that all bishops end up on the bottom row arranged in the order σ(1),σ(2),⋯,σ(2n ), from left to right.【译】设n是正整数.最开始在一个2n×2n的方格棋盘上的第一行的每个小方格内均放置一枚“象”，这些“象”从左到右依次编号：1,2,⋯,2n.定义一次“跳跃”操作为同时移动所有的“象”并满足如下条件：每一枚“象”可沿对角线方向移动任意方格；在这次“跳跃”操作结束时，所有的“象”恰在同一行的不同方格.求满足下列条件的数1,2,⋯,2n的排列σ的总个数：存在一系列的“跳跃”操作，使得结束时所有的“象”都在棋盘的最后一行，并且从左到右编号依次为：σ(1),σ(2),⋯,σ(2n ).

Let m<n be positive integers. Start with n piles, each of m objects. Repeatedly carry out the following operation: choose two piles and remove n objects in total from the two piles. For which (m ,n) is it possible to empty all the piles?【译】设正整数m<n.起初一共有n 堆石子，每堆有 m块石子. 重复执行以下操作: 选择两堆石子，从这两堆中移除共n 块石子.问：对于怎样的 (m , n)，可以移除所有石子?

Let ABC be an acute-angled triangle with AB > AC. Let P be the intersection of the tangents to the circumcircle of ABC at B and C. The line through the midpoints of line segments PB and PC meets lines AB and AC at X and Y respectively.Prove that the quadrilateral AXPY is cyclic.【译】在锐角三角形ABC中，AB>AC，△ABC的外接圆在点B和点C处的切线交于点P.一条同时过PB和PC中点的直线与AB,AC分别交于点X,Y.求证：A,X,P,Y四点共圆.

矩阵

If w is one of the imaginary cute roots of unity, show that the square of =hence show that the value of the determinant on the left is 3.

求所有的n∈N*，使得存在n阶实矩阵A,B，满足对任意的n维非零实向量v,Av,Bv线性无关.

给定素数p和正整数 n(n≥2).A为n个p阶循环群的直和.问:至少需要几个A的真子群,才能使他们的并集能覆盖A？

复矩阵A与A的任意正整数次常相似.(1)证明:A的特征值为0或 1;(2)求A的若当标准型.

设20阶实矩阵A满足eA=I20，且A在复数域上的所有特征值模长均不超过20，则这样的互不相似的A有______个.

经过抛物线焦点的弦与抛物线的轴成角θ，试证此弦在抛物线内之截线等于L/sin²⁡θ ，其中L为正焦弦之长（经过焦点而又垂直于轴之弦，称为正焦弦）.

求证：3+4cosθ+cos2θ≥0

求证：sin⁡(2nx)/(2nsinx)=cosx∙cos2x∙⋯∙cos⁡(2n-1x )

求适合sin2x+cos2x=√2 sinx及0≤x≤2π的角的值.

有连续三整数，其平方和为 50，求此三数.

线性代数

Resolve (1+52x+30x2-24x3)/(3x2-x-1)2 into partial fractions.

Factor the following:4a-16b+4a+1.

Factor the following:4(a-b)²-12(a-b)(e+9e²)

设x+y+z =0,证明: x³ +y³ +z³ = 3xyz

试求适合5x+3y>121,7/4 x+y=42 二式之x,y之值之界限.

Evaluate the determinant.

劈生数(因式分解)：3a²+a-6a²b-2b

劈生数(因式分解)：(2x+3y)²-(x-4y)²

劈生数(因式分解)：a4+a²b²+b4

解明：(6x+5)/(8x-15)-(1+8x)/15=(1-x)/3+(3-x)/5