If w is one of the imaginary cute roots of unity, show that the square of
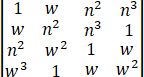 =
=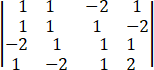
hence show that the value of the determinant on the left is 3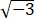 .
.
If w is one of the imaginary cute roots of unity, show that the square of
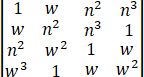 =
=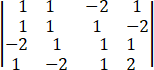
hence show that the value of the determinant on the left is 3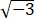 .
.
暂无答案
令A,B,C,D,E,F是三阶实方阵,且=.已知A=,B=且C=A+B-I,则[|detF|]=______.
设20阶实矩阵A满足eA=I20,且A在复数域上的所有特征值模长均不超过20,则这样的互不相似的A有______个.
求所有的n∈N*,使得存在n阶实矩阵A,B,满足对任意的n维非零实向量v,Av,Bv线性无关.
给定素数p和正整数 n(n≥2).A为n个p阶循环群的直和.问:至少需要几个A的真子群,才能使他们的并集能覆盖A?
复矩阵A与A的任意正整数次常相似.(1)证明:A的特征值为0或 1;(2)求A的若当标准型.
Find all the positive angles less than 360° which satisfy the equation:cos2x+cosx+1=0
Find the sum of the arithmetical series 49,44,39,… to 17 terms.
Find the sum of n terms of the series whose nth term is 3(4n+4n²)-5n³.
Find the general term and the sum ofn terms of the series -3,-1,11,39,89,167.
有人定酒二坛,两坛所盛斤数不等,原定一盛甲酒每斤8角,一盛乙酒每斤5角.今误将甲坛盛乙酒,乙坛盛甲酒,酒商要求加洋一元五角.问两坛斤数各几何?
若a:b=c:d,试证(a2+b2):a3/(a+b)=(c2+d2):c3/(c+d).
析a2b+ab2-a2c+ac2-2abc-b2c+bc2之因式.
若 x³ + 3px² + 3qx +r 及 x² + 2px +q 有一个一次公因子,试问 p,g,r 之间应有何种关系?又若有两个一次公因子,则其关系又若何?
化(5x²-4x+16)/((x²-x+1)²(x-3))为部分分式.
分解(x2-2x+5)/(x4-4x3+5x2-4x+4)为最简部分分式.
设 A,B 为 x 的两个有理整式,请用辗转相除法说明并证明何种情况为互质,何种情况下有公因式.有公因式时,说明求最高公因式之方法并证明之.
有理数加群(Q,+),记所有分母不超过10的有理数构成的子集为G,其对应的陪集GZ记为G ̅,则Q/Z包含G ̅的最小子群的阶为______.