如图,四棱锥P-ABCD 的底面是矩形,PD⊥底面ABCD,PD = DC = 1,M 为 BC 的中点,且 PB⊥AM.
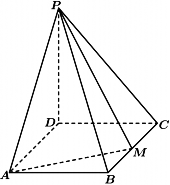
(1) 求 BC;
(2) 求二面角A-PM-B的正弦值.
如图,四棱锥P-ABCD 的底面是矩形,PD⊥底面ABCD,PD = DC = 1,M 为 BC 的中点,且 PB⊥AM.

(1) 求 BC;
(2) 求二面角A-PM-B的正弦值.
(1) 根据PD⊥平面ABCD,且四边形ABCD为矩形,不妨以点 D 为坐标原点,以 DA、DC、DP所在直线分别为 x、y、z 轴建立空间直角坐标系 D-xyz,如下图: 设BC=2a,则D(0,0,0),P(0,0,1),B(2a,1,0),M(a,1,0),A(2a,0,0),=(2a,1,-1),=(-a,1,0),∵PB⊥AM∴∙=-2a2+1=0解得:a=/2故BC=2a=.(2...
查看完整答案设2(z+z ̅)+3(z - z ̅)=4+6i,则z=【 】
在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为【 】
将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有【 】
已知a,b,c为正数,且a3/2+b3/2+c3/2=1.证明:(1)abc≤1/9;(2) a/(b+c)+b/(a+c)+c/(a+b)≤1/(2).
已知集合S={s│s=2n+1,n∈Ζ},T={t|t=4n+1,n∈Ζ},则S∩T=【 】
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍,纵坐标不变,再把所得曲线向右平移π/3个单位长度,得到函数sin(x-π/4)的图像,则f(x)=【 】
设三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=直角.求证:ABC是锐角三角形.
如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,,PA,BC的公垂线,ED=h.求证:三棱锥P-ABC的体积V=l2h/6.
如图,正三棱锥S-ABC的侧棱与底面边长相等,如果E,F分别为SC,AB的中点,那么异面直线EF与SA所成的角等于【 】
如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有【 】对。
如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S在底面射影O在△ABC内,那么O是△ABC的【 】。
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小是【 】
在正三棱锥ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为【 】
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=1/2. (I)求四棱锥S-ABCD的体积;(Ⅱ)求面SCD与面SBA所成二面角的正切值.