高考2022年全国乙·理( )
执行下面的流程图,输出的n=【 】
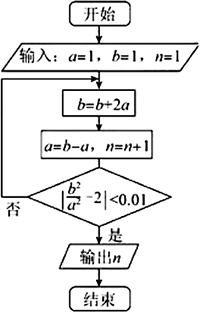
A、3
B、4
C、5
D、6
第一次循环:b=1+1×2=3,a=3-1=2,n=1+1=2,|b2/a2 -2|=|(3/2)2-2|=1/4>0.01
第二次循环:b=3+2×2=7,a=7-2=5,n=2+1=3,|b2/a2 -2|=|(7/5)2-2|=1/25>0.01
第三次循环:b=7+2×5=17,a=17-5=12,n=3+1=4,|b2/a2 -2|=|(17/12)2-2|=1/144<0.01
故输出n=4.
高考2001年上海市( )
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:①输入数据x0∈D,经数列发生器输出x1=f(x0 );②若x1∉D,则数列发生器结束工作;若x1∈D,将x1反馈回输入端,再输出x2=f(x1 ),并依此规律继续下去,现定义f(x)=(4x-2)/(x+1).
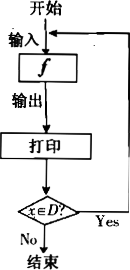
(Ⅰ)若输入x0=49/65,则由数列发生器产生数列{xn },请写出数列{xn }的所有项;
(Ⅱ)若要数列发生器生产一个无穷的常数数列,试求输入的初始数据x0的值.
(Ⅲ)若输入x0时,产生的无穷数列{xn }满足:对任意正整数n,均有xn<xn+1,求x0的取值范围.
(Ⅰ)∵f(x)的定义域D=(-∞,-1)∪(-1,+∞),
∴数列{xn },只有三项:
x1=11/19,x2=1/5,x3=-1,
(Ⅱ)∵f(x)=(4x-2)/(x+1)=x,
即x^2-3x+2=0,∴x=1或x=2.
即当x0=1或2时,xn+1=(4xn-2)/(xn+1)=xn,
故当x0=1时,xn=1
当x0=2时,xn=2(n∈N).
(Ⅲ)解不等式x<(4x-2)/(x+1),
得x<-1或1<x<2,
要使x1<x2,则x1<-1或1<x1<2
对于函数f(x)=(4x-2)/(x+1)=4-6/(x+1),
若x1<-1,则x2=f(x1 )>4,x3=f(x2 )<x2.
当1<x1<2时,x2=f(x1 )>x1,且1<x2<2,依此类推.
综上所述,x1∈(1,2),由x1=f(x0 ),得x0∈(1,2).
高考2010年上海市( )
2010年上海世博会园区每天9:00开园,20:00停止入园.在下面的框图中,S表示上海世博会官方网站在每个整点报道的入园总人数,a表示整点报道前1个小时内入园人数,则空白的执行框内应填入__________.
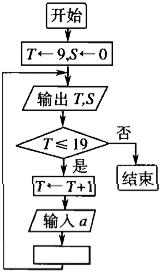
S←S+a
高考2020年江苏省( )
如图是一个算法流程图, 若输出 y 的值为 −2, 则输入 x 的值是______.
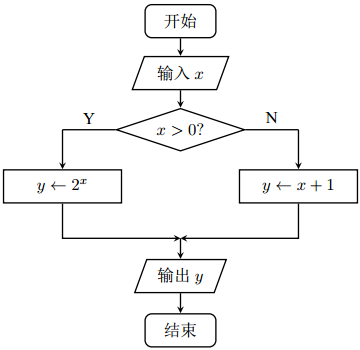
-3
高考2020年新高考Ⅱ( )
执行如图的程序框图, 若输入 k = 0, a = 0, 则输出的 k 为【 】
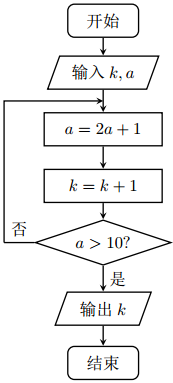
A、2
B、3
C、4
D、5

