某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了 10 件产品,得到各件产品该项指标数据如下:

旧设备和新设备生产产品的该项指标的样本平均数分别记为x ̅ 和 y ̅,样本方差分别记为S12和S22.
(1) 求x ̅ , y ̅ , S12,S22;
(2) 判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果y ̅ - x ̅ ≥2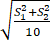 ,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高 ).
,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高 ).
某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了 10 件产品,得到各件产品该项指标数据如下:

旧设备和新设备生产产品的该项指标的样本平均数分别记为x ̅ 和 y ̅,样本方差分别记为S12和S22.
(1) 求x ̅ , y ̅ , S12,S22;
(2) 判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果y ̅ - x ̅ ≥2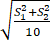 ,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高 ).
,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高 ).
(1) x ̅ =(9.8+10.3+10.0+10.2+9.9+9.8+10.0+10.1+10.2+9.7)/10=10.0, y ̅ =(10.1+10.4+10.1+10.0+10.1+10.3+10.6+10.5+10.4+10.5)/10=10.3,S12=(0.22+0.32+0+0.22+0.12+0.22+0+0.12+0...
查看完整答案以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为______ ( 写出符合要求的一组答案即可).
记△ABC的内角A,B,C的对边分别为a,b,c,面积为,B=60°,a2+c2=3ac,则b=______.
已知向量=(1,3),=(3,4),若(-λ)⊥,则λ=________.
已知双曲线x2/m - y2=1(m>0)的一条渐近线为 x+my=0,则C的焦距为________.
设B是椭圆C:x2/a2 +y2/b2 =1(a>b>0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率取值范围是【 】
设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则【 】
在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于7/4的概率为【 】
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍,纵坐标不变,再把所得曲线向右平移π/3个单位长度,得到函数sin(x-π/4)的图像,则f(x)=【 】
有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则【 】
设一组样本数据 x1, x2, · · · , xn 的方差为 0.01, 则数据 10x1, 10x2, · · · , 10xn 的方差为【 】
在一组样本数据中, 1, 2, 3, 4 出现的频率分别为 p1, p2, p3, p4, 且=1, 则下面四种情形中, 对应样本的标准差最大的一组是【 】
已知一组数据 4, 2a, 3 − a, 5, 6 的平均数为 4, 则 a 的值是______.
随机变量ξ的概率分布律由下表给出: 该随机变量ξ的均值是______.
给出20个数87 91 94 88 93 91 89 87 92 8690 92 88 90 91 86 89 92 95 88它们的和是【 】
一个袋子里装有大小相同的3个红球和2个黄球.从中同时取出2个,则其中含红球个数的数学期望是________. (用数字作答)
现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字 最小值为ξ,则 P(ξ=2)=__________,E(ξ)= _________.
有一组样本数据x1,x2,⋯,x6,其中x1是最小值,x6是最大值,则【 】
跳水比赛中,裁判给某选手的一个动作打分,其平均值为 8.6,方差为 1.1,若去掉一个最高分9.7 和一个最低分 7.3,则剩余得分的【 】