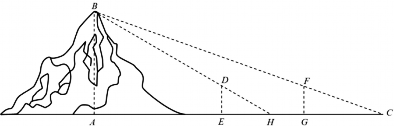
魏晋时刘徽撰写的《海岛算经》是关测量的数学著作，其中第一题是测海岛的高.如图，点E，H，G在水平线AC上，DE和FG是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG称为“表距”，GC和EH都称为“表目距”，GC与EH的差称为“表目距的差”则海岛的高AB=【 】
A、(表高×表距)/表目距的差+表高
B、(表高×表距)/表目距的差-表高
C、(表高×表距)/表目距的差+表距
D、(表高×表距)/表目距的差-表距
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
在区间(0,1)与(1,2)中各随机取1个数，则两数之和大于7/4的概率为【 】
把函数y=f(x)图像上所有点的横坐标缩短到原来的1/2倍，纵坐标不变，再把所得曲线向右平移π/3个单位长度，得到函数sin(x-π/4)的图像，则f(x)=【 】
将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有【 】
在正方体ABCD-A1B1C1D1中，P为B1D1的中点，则直线PB与AD1所成的角为【 】
设函数f(x)=(1-x)/(1+x)，则下列函数中为奇函数的是【 】
已知命题p:∃x∈R,sinx<1，命题q:∀x∈R,e|x| ≥1，则下列命题中为真命题的是【 】
已知集合S={s│s=2n+1,n∈Ζ},T={t|t=4n+1,n∈Ζ}，则S∩T=【 】
设2(z+z ̅)+3(z - z ̅)=4+6i，则z=【 】
设函数f(x)=a2x2+ax-3lnx+1，其中a>0.(1)讨论f(x)的单调性；(2)若y=f(x)的图像与x轴没有公共点，求a的取值范围.
在△ABC的边AB,AC上各取D,E点，使AD=1/3 AB,AE=1/3 AC，连结BE,CD相交于F点.求证：S△FBC=1/2 S△ABC.
设 △ABC 的重心为 G，BC、CA 的中点为 E、F，设 △ABC 的面积为 K，求△GEF 的面积.
在 △ABC 内作 AE 及 BD，假设 ∠CAE < ∠CBD，∠BAE < ∠ABD，求证 AE> BD.
△ABC 和△A'B'C'中，∠A >∠A’,则 BC >B'C'.
自 △ABC 的顶点 A 引 ∠B 的内外角平分线之垂线，则此两垂足与 AB，AC两边的中点共线.求证之.
如图，∠ABC=90°,AC=BC,AD⊥CE,BE⊥CE，垂足分别是D,E.已知AD=8,BE=3，则DE=______.