△ABC 的内角为 A, B, C 的对边分别为 a, b, c, 已知 B = 150◦.
(1) 若 a =  c, b = 2
c, b = 2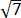 , 求 △ABC 的面积;
, 求 △ABC 的面积;
(2) 若 sin A +  sin C =
sin C = /2 , 求 C.
/2 , 求 C.
△ABC 的内角为 A, B, C 的对边分别为 a, b, c, 已知 B = 150◦.
(1) 若 a =  c, b = 2
c, b = 2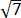 , 求 △ABC 的面积;
, 求 △ABC 的面积;
(2) 若 sin A +  sin C =
sin C = /2 , 求 C.
/2 , 求 C.
(1) 由题设及余弦定理得 28 = 3c2 + c2 − 2 ×c2 × cos 150°, 解得 c = −2(舍去) , c = 2, 从而 a = 2.故 △ABC 的面积为 1/2× 2× 2 × sin 150◦ = .(2) 在 △ABC 中, A = 180° − B ...
查看完整答案数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.
曲线 y = lnx + x + 1 的一条切线的斜率为 2, 则该切线的方程为 ________________.
设向量 a = (1, −1), b = (m + 1, 2m − 4), 若 a ⊥ b, 则 m =______ .
已知 A, B, C 为球 O 的球面上的三个点, ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π, AB = BC = AC = OO1,则球 O 的表面积为【 】
设 F1, F2 是双曲线 C : x2 −y2/3 = 1 的两个焦点, O 为坐标原点, 点 P 在 C 上且 |OP| = 2, 则 △PF1F2 的 面积为【 】
设 {an} 是等比数列, 且 a1 + a2 + a3 = 1, a2 + a3 + a4 = 2, 则 a6 + a7 + a8 =【 】
某人在高处望见正东海面上一船首,其俯角为 30°,当船向正南行 a 里后,求得船首俯角为 15°,问此人之视点高出海面若干?
曲线xy=a²上一切线与坐标轴成一三角形,求此三角形的面积.
已知三角形三边之长为 14 尺,16 尺,18 尺,求其三中线长.
当△ABC 中A为钟角时,余弦定律为 a² =b² +c² +2bccosA.
设D为△ABC一边BC之中点,证AD²=1/4(2AB²+2AC²-BC²)
有等高的两竿,自其底连线上一点望之,较近之竿的仰角为 60°,若自该点向此线之垂直方向行 80 尺而测之,得二竿之仰角为 45°,30°,试求二竿之高及其间的距离.
设人眼在墙顶上观察一塔,测得塔之全长所夹之角为θ,设墙高为h尺,墙与塔之距离为d尺.试证:(h²+d²)sinθ/(hsinθ+dcosθ)尺为塔这高.
试证三角形∠A之内角平分线之长为2bc∙cos(A/2)/(b+c).
有三角形底边长是 2a,求顶点的轨迹,使其它二边的相乘积为 a².
记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为√3,D为BC的中点,且AD=1.(1)若∠ADC=π/3,求tanB;(2)若b²+c²=8,求b,c.
若 kxy - 8x + 9y - 12 = 0 表示二条直线,求 k 值及此二直线所夹的角.
过一点 (2,1)的直线与直线 2x - 3y + 12 = 0 成45°角,求直线方程.
若三直线aix+biy+ci=0(i=1,2,3)相交于一点,则=0.试证之.
在定角 XOY 的二边上各取二点 P、Q,使 OP +OQ = a. 试求 PQ 的中点的轨迹.
试证方程 x² + 6xy + 9y² + 4x + 12y -5 = 0 之轨迹为二平行直线.
i) 设直线ax+by+c=0,经过点(5,-4).求其系数a,b,c须满足的条件.ii)设直线ax+by+c=0,至原点之距离为 1,求其系数a,b,c须满足的条件.
已知一点 A(-1,-2),求至椭圆 x² + 5y² = 5 的切线方程.
过点(0,-2)与圆x²+y²-4x-1=0相切的两条直线的夹角为α,则sinα=【 】
已知直线l:x-my+1=0与⨀C:(x-1)²+y²=4交于A,B两点,写出满足“△ABC的面积为8/5”的m的一个值______.