高中数学-高考试题(全国统考 1984年变化率与导数)

问答题（1984年全国统考）

如图，已知圆心为O、半径为1的圆与直线l相切于点A，一动点P自切点A沿直线l向右移动时，取弧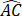的长为2/3AP，直线PC与直线AO交于点M.又知当AP=3π/4时，点P的速度为v，求这时点M的速度.

答案解析

作CD⊥AM,并设AP=x,AM=y,∠COD=θ.由假设, (AC) ̂的长为2/3 AP=2/3 x,半径OC=1,可知θ=2/3 x.考虑x∈(0,π).∵ △APM∼△DCM,∴ AM/AP=DM...

查看完整答案

讨论

高中数学

设a>2，给定数列{xn},其中x1 = a,xn+1=(xn2)/(2(xn-1)) (n=1,2,…),求证：(1) xn>2,且xn+1/xn < 1(n=1,2,…);(2) 如果a≤3,那么xn ≤ 2+1/2n-1 (n=1,2,…);(3) 如果a>3,那么当n ≥ (lga/3)/(lg4/3)时，必有xn+1<3.

在△ABC中，∠A,∠B,∠C所对的边分别为a,b,c,且c=10, cosA/cosB=b/a=4/3, P为△ABC的内切圆上的动点.求点P到顶点A,B,C的距离的平方和的最大值与最小值.

求经过定点M(1,2),以y轴为准线,离心率为1/2的椭圆的左顶点的轨迹方程.

设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.

设c,d,x为实数，c≠0,x为未知数.讨论方程 = -1在什么情况下有解.有解时求出它的解.

已知三个平面两两相交，有三条交线.求证这三条交线交于一点或互相平行.

画出极坐标方程(ρ-2)(θ-π/4)=0(ρ>0)的曲线.

设,画出函数y=H(x-1)的图像.

要排一张有6个歌唱节目和4个舞蹈节目的演出节目单，任何两个舞蹈节目不得相信，问：有多少种不同的排法？（只要写出式子，不必计算）

全国统考数列与推理

变化率与导数

函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【】。

设函数 f(x) = x3 + bx + c, 曲线 y = f(x) 在点 (1/2 , f(1/2))处的切线与 y 轴垂直.(1) 求 b;(2) 若 f(x) 有一个绝对值不大于 1 的零点, 证明: f(x) 的所有零点的绝对值都不大于 1.

已知函数 f(x)=x3+klnx (k ∈ R) , f′(x) 为 f(x) 的导函数.(I) 当 k = 6 时,(i) 求曲线 y = f(x) 在点 (1, f(1)) 处的切线方程;(ii) 求函数 g(x)=f(x)+f'(x)+9/x 的单调区间和极值;(II) 当 k ⩾ −3 时, 求证: 对任意的 x1, x2 ∈ [1, +∞), 且 x1 > x2, 有f'(x1+x2)/2 > (f(x1 )-f(x2))/(x1-x2 ) .

在复平面内，把复数3-i对应的向量按顺序时针方向旋转π/3，所得向量对应的复数是【】

已知复数z1=i⁡(1-i)3.(Ⅰ)求argz1及|z1|；(Ⅱ)当复数z满足|z|=1，求|z - z1|的最大值.

已知z=1+i.(Ⅰ)设ω=z2+3z ̅-4，求ω的三角形式；(Ⅱ)如果=1-i，求实数a,b的值.

不等式>3-2x的解集是__________.

解不等式 loga⁡(1-1/x)>1.

不等式组的解集是【】

已知复数z=/2 - 1/2 i,ω=/2+/2 i.复数,z2ω3在复数平面上所对应的点分别为P,Q.证明△OPQ是在等腰直角三角形（其中O为原点）.

导数与微分

不大于log2⁡(x3+1)dx+(2x-1)1/3dx的最大整数是______.

设β=，则6β的值为______.

设函数 f(x) = ex/(x+a). 若 f′(1) = e/4 , 则 a = ______.

利用积分计算椭圆x2/a2 +y2/b2 =1(a>b>0)所围成的面积.

写出曲线y=ln⁡|x|过坐标原点的切线方程：____________，____________．

当x=1时，函数f(x)=a ln⁡x+b/x取得最大值-2，则f'(2)=【】

已知函数f(x)=x3-x,g(x)=x2+a，曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线．（1）若x1=-1，求a；（2）求a的取值范围．

已知x=x1和x=x2分别是函数f(x)=2ax-e⁡x2（a>0且a≠1）的极小值点和极大值点．若x1<x2，则a的取值范围是____________．

已知函数f(x)=ln⁡(1+x)+axe-x（1）当a=1时，求曲线y=f(x)在点(0,f(0))处的切线方程；（2）若f(x)在区间(-1,0),(0,+∞)各恰有一个零点，求a的取值范围．

已知函数f(x)=ax-1/x-(a+1)ln⁡x．（1）当a=0时，求f(x)的最大值；（2）若f(x)恰有一个零点，求a的取值范围．