已知关于 x 的函数 y = f(x), y = g(x) 与 h(x) = kx + b (k, b ∈ R) 在区间 D 上恒有 f(x) ⩾ h(x) ⩾ g(x).
(1) 若 f(x) = x2 + 2x, g(x) = −x2 + 2x, D = (−∞, +∞), 求 h(x) 的表达式;
(2) 若 f(x) = x2 − x + 1, g(x) = k ln x, h(x) = kx − k, D = (0, +∞), 求 k 的取值范围;
(3) 若 f(x) = x4−2x2, g(x) = 4x2−8, h(x) = 4(t3−t)x−3t4+2t2 (0 < |t| ⩽ ), D = [m, n] ⊂ [-
), D = [m, n] ⊂ [- ,
,  ].
].
求证: n − m ⩽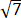 .
.
(1) 由 f(x)=g(x) 得 x=0. 又f' (x)=2x+2,g' (x)=-2x+2, 所以 f' (0)=g' (0)=2.所以, 函数 h(x) 的图像为过原点, 斜率为 2 的直线, 所以 h(x)=2x. 经检验, h(x)=2x 符合题意.(2) h(x)-g(x)=k(x-1-lnx).设 φ(x)=x-1-lnx, 则 φ' (x)=1-1/x=(x-1)/x; φ(x)≥φ(1)=0. 所以当 h(x)-g(x)≥0 时, k≥0.由f(x)-h(x)=x2-x+1-(kx-k)=x2-(k+1)x+(1+k)≥0,得:当 x=k+1≤0 时, f(x) 在 (0,+∞) 上递增, 所以 f(x)=1+k≥0, 所以k=-1.当 k+1>0 时, ∆≤0, 即 (k+1)2-4(k+1)≤0,(k+1)(k-3)≤0,-1<k≤3.综上, k ∈ [0, 3] .(3) 因为 f(x)=x4-2x2, 所以 f' (x)=4x3-4x=4x(x+1)(x-1)...
查看完整答案 ), D = [m, n] ⊂ [-
), D = [m, n] ⊂ [- ,
,  ].
].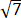 .
.
