高中数学-高考试题(浙江省 2022年解三角形)

填空题（2022年浙江省）

我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是S=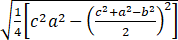，其中a，b，c是三角形的三边，S是三角形的面积．设某三角形的三边a=√2,b=√3,c=2，则该三角形的面积S=___________．

答案解析

/4

【解析】

根据“三斜求积”公式：S=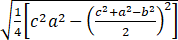==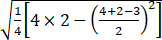/4

讨论

三角形

△ABC 和△A'B'C'中，∠A >∠A’,则 BC >B'C'.

自 △ABC 的顶点 A 引 ∠B 的内外角平分线之垂线，则此两垂足与 AB，AC两边的中点共线.求证之.

设ABC是一个正三角形.点A1,B1,C1在三角形ABC的内部，且满足A1 B=A1 C,B1 A=B1 C,C1 A=C1 B及∠BA1 C+∠CB1A+∠AC1 B=480°.设直线BC1与CB1交于点A2，AC1与A1 C交于B2，AB1与A1 B交于C2.证明：若三角形A1 B1 C1的三边长度两两不等，则三角形AA1 A2,BB1 B2,CC1 C2的外接圆都经过两个公共点.

如图，∠ABC=90°,AC=BC,AD⊥CE,BE⊥CE，垂足分别是D,E.已知AD=8,BE=3，则DE=______.

在锐角三角形ABC中，AB<AC.设Ω为三角形ABC的外接圆.点S是Ω上包含点A的弧BC的中点.过点A作垂直于BC的直线与BS交于点D,与圆Ω交于另一点E,E≠A.过点D且平行于BC 的直线与直线BE交于点L.记ω为三角形BDL的外接圆.设ω与Ω交于另一点P,P≠B.证明：ω在点P处的切线与直线BS的交点在∠BAC的内角平分线上.

Consider the convex quadrilateral ABCD. The point P is in the interior of ABCD. The following ratio equalities hod:∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.Prove that the following three lines meet in a point : the internal bisectors of angles ∠ADP and ∠PCB and the perpendicular bisector of segment AB.设P是凸四边形ABCD内部一点，且满足：∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.证明：∠ADP的内角平分线、∠PCB的内角平分线和线段AB的中垂线，三线共点。（波兰供题）

已知△ABC三内角的大小成等差数列，tanAtanC=2+，求角A，B，C的大小；又知顶点C的对边c上的高等于4，求三角形各边a，b，c的长.（提示：必要时可验证(1+)2=4+2）

叙述并证明勾股定理.

CD为直角三角形ABC中斜边AB上的高，已知△ADC,△CBD,△ABC的面积成等比数列，求∠B(用反三角函数表示).

锐角△ABC中，AB>AC，M为其外接圆⊙O的劣弧BC的中点，K为A的对径点，过O作OD∥AM交AB于D，交CA的延长线于E，直线BM交直线CK于P，直线CM交直线BK于Q. 求证：∠OPB+∠OEB=∠OQC+∠ODC.

解三角形

△ABC 的内角 A, B, C 的对边分别为 a, b, c, 已知 cos2(π/2 + A) + cos A = 5/4.(1) 求 A.(2) b − c =/3a, 证明: △ABC 是直角三角形.

在 △ABC 中, cosC =2/3, AC = 4, BC = 3, 则 tanB =【】

已知向量 a, b 满足 |a| = 5, |b| = 6, a · b = −6, 则 cos⟨a, a + b⟩ =【】

在 △ABC 中, cosC = 2/3 , AC = 4, BC = 3, 则 cosB =【】

在 ① ac =, ② csin A = 3, ③ c = b 这三个条件中任选一个, 补充在下面问题中, 若问题中的三角形存在, 求 c 的值; 若问题中的三角形不存在, 说明理由.问题：是否存在 △ABC, 它的内角 A, B, C 的对边分别为 a, b, c, 且 sinA = sinB, C = π/6 ,__________?注：如果选择多个条件分别解答, 按第一个解答计分.

在 △ABC 中, a + b = 11, 再从条件 ①、条件 ② 这两个条件中选择一个作为已知, 求:(I) a 的值;(II) sin C 和 △ABC 的面积.条件 ①: c = 7, cos A = -1/7;条件 ②: cos A = 1/8, cos B = 9/16.注：如果选择条件 ① 和条件 ② 分别解答, 按第一个解答计分.

在 △ABC 中, 角 A, B, C 所对的边分别为 a, b, c. 已知 a = 2√2, b = 5, c = .(I) 求角 C 的大小;(II) 求 sin A 的值;(III) 求 sin⁡(2A+π/4) 的值.

在锐角 △ABC 中, 角 A, B, C 的对边分别为 a, b, c, 且 2bsinA − a = 0.(I) 求角 B;(II) 求 cosA + cosB + cosC 的取值范围.

设等腰△OAB的顶角为 2θ，高为h.(1) 在△OAB内有一动点P，到三边OA,OB,AB的距离分别为|PD|,|PF|,|PE|，并且满足关系式|PD|∙|PF|=|PE|2，求P点的轨迹.(2) 在上述轨迹中定出点P的坐标，使得|PD|+|PE|=|PF|.

某人要作一个三角形，要求它的三条高的长度分别是1/13 ，1/11 ，1/5 ，则此人将【】

平面解析几何

已知向量a=(2,1)，b=(-2,4)，则|a-b|=【】

若直线2x+y-1=0是圆(x-a)2+y2=1的一条对称轴，则a=【】

在△ABC中，AC=3,BC=4,∠C=90°．P为△ABC所在平面内的动点，且PC=1，则(PA)⋅(PB)的取值范围是【】

设二斜交轴 x 与y 交角为 θ，作一圆使通过 x 轴上之二定点 (a²,0),(b²,0)且与 y 轴相切，求此圆之方程式.

一圆与二坐标轴及直线 x=a相切，求其方程.

已知向量a ̅=(1,1),b ̅=(1,-1).若(a ̅+λb ̅)⊥(a ̅+μb ̅)，则【】

已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1)，则|a→ |²-|b→ |²=【】

在平面内, A, B 是两个定点, C 是动点. •= 1, 则点 C 的轨迹为【】

点 (0, −1) 到直线 y = k(x + 1) 距离的最大值为【】

己知椭圆 C : x2/25 + y2/m2 = 1 (0 < m < 5) 的离心率为 , A, B 分别为 C 的左、右顶点.(1) 求 C 的方程;(2) 若点 P 在 C 上, 点 Q 在直线 x = 6 上, 且 |BP| = |BQ|, BP⊥BQ, 求 △APQ 的面积.