高中数学-高考试题(全国乙·文 2022年平面向量)

单项选择（2022年全国乙·文）

已知向量a=(2,1)，b=(-2,4)，则|a-b|=【】

A、2

B、3

C、4

D、5

答案解析

D

【解析】

因为a-b=(2,1)-(-2,4)=(4,-3)，

所以|a-b |=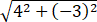=5.

讨论

高中数学

设(1+2i)a+b=2i，其中a,b为实数，则【】

集合M={2,4,6,8,10},N={x|-1<x<6}，则M∩N=【】

已知a,b,c为正数，且a3/2+b3/2+c3/2=1.证明：(1)abc≤1/9;(2) a/(b+c)+b/(a+c)+c/(a+b)≤1/(2).

在直角坐标系xOy中，曲线C的方程为（t为参数）.以坐标原点为极点，x轴正半轴为极轴建立坐标系，已知直线l的极坐标方程为ρsin⁡(θ+π/3)+m=0.(1) 写出l的直角坐标方程；(2) 若l与C有公共点，求m的取值范围.

已知函数f(x)=ln⁡(1+x)+axe-x（1）当a=1时，求曲线y=f(x)在点(0,f(0))处的切线方程；（2）若f(x)在区间(-1,0),(0,+∞)各恰有一个零点，求a的取值范围．

已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过A(0,-2),B(3/2,-1)两点．（1）求E的方程；（2）设过点P(1,-2)的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满足(MT)→=(TH)→．证明：直线HN过定点.

某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：m2）和材积量（单位：m3），得到如下数据：并计算得xi2 =0.038,yi2 =1.6158,xiyi=0.2474．（1）估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；（2）求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；（3）现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为186m2．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值．附：相关系数r= ,≈1.377．

如图，四面体ABCD中，AD⊥CD,AD=CD,∠ADB=∠BDC，E为AC的中点．（1）证明：平面BED⊥平面ACD；（2）设AB=BD=2,∠ACB=60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．

记△ABC的内角A,B,C的对边分别为a,b,c，已知sin⁡Csin⁡( A-B)=sin⁡Bsin⁡(C-A)．（1）证明：2a2=b2+c2；（2）若a=5,cos⁡A=25/31，求△ABC的周长．

已知x=x1和x=x2分别是函数f(x)=2ax-e⁡x2（a>0且a≠1）的极小值点和极大值点．若x1<x2，则a的取值范围是____________．

平面向量

已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则• 的取值范围是【】

已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .

如图, 在四边形 ABCD 中, ∠B = 60º, AB = 3, BC = 6, 且 =λ, ·= -3/2, 则实数 λ 的值为_____, 若 M, N 是线段 BC 上的动点, 且 || = 1, 则· 的最小值为______.

设 k ∈ N∗, 已知平面向量 a1, a2, b1, b2, · · · , bk 两两不同, |a1 − a2| = 1. 对于任意 i = 1, 2, j = 1, 2, 3,· · · , k, |ai − bj| ∈ {1, 2}, 则 k 的最大值是_______________.

已知单位向量 e1, e2 满足|e1-e2 |≤, 设 a = e1 + e2, b = 3e1 + e2, 向量 a, b 的夹角为 θ, 则 cos2θ的最小值为_______.

在 △ABC 中, AB = 4, AC = 3, ∠BAC = 90º, D 在边 BC 上, 延长 AD 到 P , 使得 AP = 9. 若=m+(3/2-m) (m 为常数), 则 CD 的长度是__________.

如图所示，直线x=2 与双曲线 Γ: x2/4 - y2=1的渐进线交于E1, E2两点，记=e1,=e2.任取双曲线Γ上的点P，若 = ae1+be2 （a,b∈R)，则a,b满足的一个等式是_______.

设a,b,c是任意的非零平面向量，且相互不共线，则①(a∙b)c-(c∙a)b=0②|a|-|b|<|a-b|③(b∙c)a-(c∙a)b不与c垂直④(3a+2b)∙(3a-2b)=9|a|2 - 4|b|2 中，是真命题的有【】

已知向量=(-1,2),=(3,m)，若⊥，则m=________.

若向量a=(1,1),b=(1,-1),c=(-1,2)，则c=【】

平面解析几何

已知半径为 1 的圆经过点 (3, 4), 则其圆心到原点的距离的最小值为【】

已知直线 x − y + 8 = 0 和圆 x2 + y2 = r2 (r > 0) 相交于 A, B 两点. 若 |AB| = 6, 则 r 的值为______.

在平面直角坐标系 xOy 中, 已知 P(/2,0), A、 B 是圆 C : x2+(y-1/2)2=36上的两个动点, 满足 P A = P B, 则 △P AB 面积的最大值是______.

用解析几何方法证明三角形的三条高线交于一点.

如果圆x2+y2+Gx+Ey+F=0与x轴相切于原点，那么【】。

在△ABC中，∠A,∠B,∠C所对的边分别为a,b,c,且c=10, cosA/cosB=b/a=4/3, P为△ABC的内切圆上的动点.求点P到顶点A,B,C的距离的平方和的最大值与最小值.

圆C：x2+y2-2x-4y+4=0的圆心到直线3x+4y+4=04的距离d=_____.

已知两点P(-2,2),Q(2,2)以及一条直线l:y=x.设长为的线段AB在直线l上移动.求直线PA和QB的交点M的轨迹方程.(要求把结果写成普通方程)

如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)所表示的曲线关于y=x对称，那么必有【】

设圆M的方程为(x-3)2+(y-2)2=2，直线l的方程为x+y-3=0，点P的坐标为(2,1)，那么【】