高中数学-高考试题(武汉大学 1949年圆锥曲线)

问答题（1949年武汉大学）

判别曲线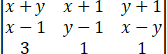=0的性质.

答案解析

暂无答案

讨论

行列式

试证=(sin⁡(c-a)sin⁡(a-b))/sin⁡(b+c) · [-2 sin⁡(b+c) sin⁡(b-c) ]=-2sin⁡(b-c)sin⁡(c-a)sin⁡(a-b)

北京大学行列式

若A+B+C=180°，求证=0

浙江大学行列式

若α=cos20°,b=cos40°,c=cos80°，试求行列式之数值.

已知齐次方程组式中A,B,C为三参数.(1)求此方程组x=y=z=0之一组解答外，有其他解答时A,B,C间之关系.(2)求证A+B+C=π时，x,y,z恰为一三角形之三边.

定义方程g:[0,π/2]→R为g(θ)=+，其中f(θ)=1/2 +设一元二次函数p(x)的根为方程g(θ)的最大值与最小值，若p(2)=2-√2，则以下说法正确的是【】

非零实数p,q,r分别为调和数列的第10、第100和第1000项，考虑线性方程组列Ⅰ 列Ⅱ(Ⅰ)若q/r=10，则方程组 (P) 有解x=0,y=10/9,z=-1/9(Ⅱ) 若p/r≠100，则方程组 (Q) 有解x=10/9,y=-1/9,z=0(Ⅲ) 若p/q≠10，则方程组 (R) 无穷多解(Ⅳ) 若p/q=10，则方程组 (S) 无解 (T)至少1个解正确的选项为【】

试解下列之联立方程式，求x,y,z之值

山东大学行列式

圆锥曲线

已知椭圆方程x2/a2 +y2/b2 =1,F为右焦点，A为右顶点，B为上顶点，|BF|/|AB| =√3/2.(1)求椭圆的离心率e；(2)已知直线l与椭圆有唯一交点M，直线l交y轴于点N,|OM|=|ON|,∆OMN的面积为√3,求椭圆的标准方程.

已知抛物线y2=4√5 x,F1,F2分别是双曲线x2/a-y2/b=1(a>0,b>0)的左右焦点，抛物线的准线过双曲线的左焦点F1，与双曲线的渐近线交于点A,，若∠F1 F2 A=π/4，则双曲线的标准方程是【】

英：Find the equations to the tangents to the ellipse 3x²+ y² = 3, inclined at angle of 45° to the axis of x.汉：求椭圆 3x²+y²=3之与x轴夹角为 45°的切线方程.

英：Find the equation to the normal to hyperbola x2/a2 -y2/b2 =1 at the point (x1,y1) . 汉：求双曲线x2/a2 -y2/b2 =1在点(x1,y1)处的法线方程.

The point of contact of a tangent to an hyperbola is midway between the points in which the tangent meets the asymptotes.

Find the locus of the point of intersection of lines drawn through the foci of an ellipse parallel to conjugate diameters.

双曲线之切线与渐近线相交，试证切点移动其所包围之三角形之面积为常数.

Find the area of the triangle out off from the first quadrant by the tangent to the ellipse 2x² + 3y² = 14 at the point (1, 2).

Reduce the hyperbola 4x² - 9y² - 24x + 36y - 36 = 0 to standard form.

双曲线x²/100-y²/64=1的焦点为S,S1;，其中S位于x正半轴上. P为双曲线在第一象限上的一点，记∠SPS1=α,α<π/2. 过点S且斜率与双曲线在P点切线相同的直线，与直线S1 P交于P1点，记P到直线SP1的距离为δ,β=S1 P.则不超过βδ/9 sin⁡α/2的最大整数为______.

平面解析几何

在△ABC中，已知a=3,b=2c.(1)若A=2π/3，求S△ABC.(2) 若2sinB-sinC=1，求C△ABC.

在边长为1的等边三角形ABC中，D为线段BC上的动点，DE⊥AB且交AB于点E,DF//AB交AC于点F，则|2+|的值为__________；(+)∙最小值为__________.

已知平面向量,,(≠0)满足| |=1,| |=2,∙=0,(- )∙=0.记向量在,方向上的投影分别为x,y,-在方向的投影为z，则x2+y2+z2的最小值为________.

已知a,b,c分别表示△ABC的角A,B,C对边的长，求证：a(sinB-sinC)+b(sinC-sinA)+c(sinA-sinB)=0.

已知△ABC，若对任意t∈R,|(BA)→-t(BC)→ |≥|(AC)→|，则△ABC一定为【】。

在△ABC中，点D在边AB上，BD=2DA.记=m,=n，则=【】

已知a→=(3,4),b→=(1,0),c→=a→+tb→，若<a→,c→>=<b→,c→>，则t=【】

设向量a，b的夹角的余弦值为1/3，且|a|=1，|b|=3，则(2a+b)⋅b=_________．

已知△ABC中，点D在边BC上，∠ADB=120°,AD=2,CD=2BD．当AC/AB取得最小值时，BD=________．

已知向量a=(m,3),b=(1,m+1)．若a⊥b，则m=__________．