高中数学-高考试题(上海市 2022年行列式)

填空题（2022年上海市）

已知a∈R，行列式的值与行列式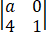的值相等，则a=________.

答案解析

3

【解析】

展开行列式：=2a-3,=a，

∵两行列式值相等，

∴2a-3=a⟹a=3.

讨论

高中数学

函数f(x)=cos2⁡x-sin2⁡x+1的周期为________.

双曲线x2/9-y2=1的实轴长为________.

已知z=1+i（其中i为虚单位），则2z ̅=________.

设函数f(x)=e/2x+ln⁡x (x>0)．（1）求f(x)的单调区间；（2）已知a,b∈R，曲线y=f(x)上不同的三点(x1,f(x1 )),(x2,f(x2 )),(x_3,f(x_3 ))处的切线都经过点(a,b)．证明：（ⅰ）若a>e，则0<b-f(a)<1/2 (a/e-1)；（ⅱ）若0<a<e,x1<x2<x_3，则2/e+(e-a)/(6e2 )<1/x1 +1/x_3 <2/a-(e-a)/(6e2 )．（注：e=2.71828⋯是自然对数的底数）

如图，已知椭圆x2/12+y2=1．设A，B是椭圆上异于P(0,1)的两点，且点Q(0,1/2)在线段AB上，直线PA,PB分别交直线y=-1/2 x+3于C，D两点．（1）求点P到椭圆上点的距离的最大值；（2）求|CD|的最小值．

已知等差数列{an}的首项a1=-1，公差d>1．记{an}的前n项和为Sn(n∈N* )．（1）若S4-2a2 a3+6=0，求Sn；（2）若对于每个n∈N*，存在实数cn，使an+cn,an+1+4cn,an+2+15cn成等比数列，求d的取值范围．

如图，已知ABCD和CDEF都是直角梯形，AB//DC，DC//EF，AB=5，DC=3，EF=1，∠BAD=∠CDE=60°，二面角F-DC-B的平面角为60°．设M，N分别为AE,BC的中点．（1）证明：FN⊥AD；（2）求直线BM与平面ADE所成角的正弦值．

在△ABC中，角A，B，C所对的边分别为a，b，c．已知4a=√5 c,cos⁡C=3/5．（1）求sin⁡A的值；（2）若b=11，求△ABC的面积．

设点P在单位圆的内接正八边形A1A2…A8的边A1A2上，则(PA1)2+(PA2)2+⋯+(PA8)2的取值范围是_______．

已知双曲线x2/a2 -y2/b2 =1(a>0,b>0)的左焦点为F，过F且斜率为b/4a的直线交双曲线于点A(x1,y1 )，交双曲线的渐近线于点B(x2,y2 )且x1<0<x2．若|FB|=3|FA|，则双曲线的离心率是_________．

行列式

设x>y>z，证明：1/(yz+zx+xy) <0.

行列式的值是______.

在n行n列矩阵中，记位于第i行第j列的数为 aij (i,j=1,2,...,n).当n=9时，a11+a22+a33+...a99=________.

设β为实数，矩阵A=.若A7-(β-1) A6-βA5为奇异矩阵，则9β的值为______.

北京大学行列式

若A+B+C=180°，求证=0

浙江大学行列式

已知齐次方程组式中A,B,C为三参数.(1)求此方程组x=y=z=0之一组解答外，有其他解答时A,B,C间之关系.(2)求证A+B+C=π时，x,y,z恰为一三角形之三边.

清华大学行列式

若α,β,γ为方程x³+ax²+bx+c=0之根，试求行列式D=的值，但不许展开此行列式.

线性代数

将f(x)=x³-3x²+5x+6的根增一常数，使变后的方程缺x²项.

试从x=by+cz,y=cz+ax,z=ax+by，消去x,y,z.求a,b,c间的关系式.

化(5x²-4x+16)/((x²-x+1)²(x-3))为部分分式.

求下式之部分分式(2x+3)/((x-2)(x²+3)).

分解(x2-2x+5)/(x4-4x3+5x2-4x+4)为最简部分分式.

设 A,B 为 x 的两个有理整式，请用辗转相除法说明并证明何种情况为互质，何种情况下有公因式.有公因式时，说明求最高公因式之方法并证明之.

求所有的n∈N*，使得存在n阶实矩阵A,B，满足对任意的n维非零实向量v,Av,Bv线性无关.

给定素数p和正整数 n(n≥2).A为n个p阶循环群的直和.问:至少需要几个A的真子群,才能使他们的并集能覆盖A？

复矩阵A与A的任意正整数次常相似.(1)证明:A的特征值为0或 1;(2)求A的若当标准型.

A polynomial P with integer coefficients is square-free if it is not expressible in the form P=Q² R, where Q and R are polynomials with integer coefficients and Q is not constant. For a positive integer n, let Pn be the set of polynomials of the form1+a1 x+a2 x²+⋯+an xnwith a1,a2,⋯,an∈{0,1}. Prove that there exists an integer N so that, for all integers n>N, more than 99% of the polynomials in Pn are square-free.【译】我们称整系数多项式P是无平方因子的，如果其不能表示为P=Q² R的形式，这里Q,R为整系数多项式且Q不为常数.对于正整数n，记Pn为如下形式的多项式组成的集合：1+a1 x+a2 x²+⋯+an xn这里a1,a2,⋯,an∈{0,1}.证明：存在整数N，使得对任意的整数n≥N,Pn中超过99%的多项式都是无平方因子的.