高中数学-高考试题(北京市 2022年复数的运算)

单项选择（2022年北京市）

若复数z满足i⋅z=3-4i，则|z|=【】

A、1

B、5

C、7

D、25

答案解析

B

【解析】

等式i⋅z=3-4i两端同乘以i，得-z=3i+4，即z=-4-3i，

所以|z|=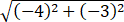=5.

讨论

高中数学

已知全集U={ x|-3<x<3}，集合A={ x|-2<x≤1}，则∁UA=【】

已知函数f(x)=ax-1/x-(a+1)ln⁡x．（1）当a=0时，求f(x)的最大值；（2）若f(x)恰有一个零点，求a的取值范围．

记△ABC的内角A，B，C的对边分别为a，b，c﹐已知sin⁡C sin⁡(A-B)=sin⁡Bsin⁡(C-A)．（1）若A=2B，求C；（2）证明：2a2=b2+c2.

若f(x)=ln⁡|a+1/(1-x)|+b是奇函数，则a=_____，b=______．

记Sn为等差数列{an}的前n项和．若2S3=3S2+6，则公差d=__________．

函数f(x)=cos⁡x+(x+1)sin⁡x+1在区间[0,2π]的最小值、最大值分别为【】

设F为抛物线C:y2=4x的焦点，点A在C上，点B(3,0)，若|AF|=|BF|，则|AB|=【】

已知等比数列{an}的前3项和为168，a2-a5=42，则a6=【】

如图是下列四个函数中的某个函数在区间[-3,3]的大致图像，则该函数是【】

若x,y满足约束条件，则z=2x-y的最大值是【】

复数的运算

若 z = 1 +i，则|z2 −2z| =【】

若 z = 1 + 2i+i3, 则|z| =【】

设复数 z1, z2 满足 |z1| = |z2| = 2, z1 + z2 = + i , 则 |z1 − z2| =______.

(2-i)/(1+2i) =【】

i 是虚数单位, 复数 (8-i)/(2+i) = ________.

若复数z=1-2i(i为虚数单位),则z·z ̅+z=_____.

已知ω=(-1-i)/2，求ω2+ω+1的值.

设复数z1和z2满足关系式=0，其中A为不等于0的复数.证明：(1)| z1+A||z2+A|=|A|2;(2) =||.

((1-i)/(1+i))2的值等于【】

设复数z满足关系式z+|z ̅|=2+i，那么z等于【】

数系与复数

用数学归纳法证明等式对一切自然数n都成立.

设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.

设O为复平面的原点，Z1和Z2为复平面内的两个动点，且满足：(Ⅰ) Z1和Z1所对应的复数的辐角分别为定值θ和-θ (0<θ<π/2);(Ⅱ) △OZ1 Z2的面积为定值S.求△OZ1 Z2的重心Z所对应的复数的模的最小值.

在复平面内，若复数z满足|z+1|=|z-i|，则z所对应的点Z的集合构成的图形是【】

设a≥0，在复数集C中解方程z2+2|z|=a.

设{zn } (n≥1)是复数数列，奇数项为实数，偶数项为纯虚数，且∀k∈N+,|zkzk+1| = 2k，记fn=|z1 + z2 + ⋯ + zn |.(1) 求f2020的最小可能值；(2) 求f2020∙f2021的最小可能值.

复平面上点A,B对应的复数分别为z1=2,z2=-3，点P对应的复数为z,(z-z1)/(z-z2 )的辐角主值为φ.当点P在以原点为圆心，1为半径的上半圆周（不包括两个端点）上运动时，求φ的最小值.

已知z1,z2是两个给定的复数，且z1≠z2，它们在复平面上分别对应于点Z1和点Z2.如果z满足方程|z-z1|-|z-z2|=0,那么z对应的点Z的集合是【】

在复平面上，一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O(其中O为原点)，已知Z2对应复数z2=1+i，求Z1和Z3对应的复数.

设复数z=3cosθ+i∙sinθ.求函数y=θ-argz(0<θ<π/2)的最大值以及对应的θ值.