高中数学-高考试题(上海市 1990年长方体)

单项选择（1990年上海市）

设过长方体同一个顶点的三个面的对角线长分别是a,b,c，那么这个长方体的对角线长是【】

A、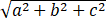

B、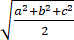

C、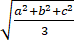

D、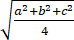

答案解析

B

讨论

高中数学

设α角属于第Ⅱ象限，且|cos α/2|=-cos α/2，则α/2角属于【】

设2a = 3,2b = 6,2c = 12，则a,b,c【】

设点P在有向线段的延长线上，P分所成的比为λ，则【】

函数f(x)和g(x)的定义域均为R，“f(x),g(x)都是奇函数”是“f(x)与g(x)的积是偶函数”的【】

圆的半径是1，圆心极坐标是(1,0)，则这个圆的极坐标方程是【】

平面上，四条平行直线与另外五条平行直线互相垂直，则它们构成的矩形共有______个（结果用数值表示）.

双曲线2mx2 - my2 = 2的一条准线是y=1，则m=______.

已知(x+a)7的展开式中，x4的系数是-280，则a=______.

已知圆锥的中截面周长为a，母线长为l，则它的侧面积等于______.

设复数ω = cos(2π/5) + isin(2π/5)，则ω + ω2 + ω3 + ω4 + ω5的值是________.

立体几何

如果正方体ABCD-A′B′C′D′的棱长为a，则A′-ABD的体积是【】

如下图所示,在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB, 将剩余部分沿OC,OD折叠，使OA,OB重合，则A(B),C,DCO为顶点的四面体的体积是_______.

如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积.

如果圆锥的底面半径为，高为2，那么它的侧面积是【】

如图，在平行六面体ABCD-A1B1C1D1中，已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=π/3. (Ⅰ)求证：顶点A1在底面ABCD的射影O在∠BAD的平分线上；(Ⅱ)求这个平行六面体的体积.

设P是一个凸多面体，满足以下两个性质：(i) P的每一个顶点恰属于 3 个不同的面；(ii) 对任意 k ≥3， P 中 k 边形面都恰有偶数个。有一只蚂蚁从某条棱的中点出发，沿棱爬行，走一条闭合路径 L ，经过 L 上每一点恰好一次，最终回到出发点。 L 将 P 的表面分为两部分，使得对任意的 k ≥3，两部分中 k 边形面的个数相等。求证：蚂蚁在爬行中向左转和向右转的次数相等。

已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为【】

如图，长方体ABCD-A1 B1 C1 D1中，已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点，求三棱锥C-PAD的体积；(2)求直线AB1与平面ACC1 A1的夹角大小.

某几何体的三视图如图所示，则该几何体的体积是【】

甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S甲和S乙，体积分别为V甲和V乙．若S甲/S乙 =2，则V甲/V乙 =【】

长方体

有长方体积之冰块，其长 2 步，阔 1 步 3 尺，厚4 尺，而此冰之比重为 0.93，若置其于水中，浮出水面之高几寸?

一个长方体共一顶点的三个面的面积分别是,, ,这个长方体对角线的长是【】

建造一个容积为8m3，深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为________元。

长方体的全面积为11,12条棱长度之和为24,则这个长方体的一条对角线长为【】

对任意函数f(x),x∈D，可按图示构造一个数列发生器，其工作原理如下：①输入数据x0∈D，经数列发生器输出x1=f(x0 )；②若x1∉D，则数列发生器结束工作；若x1∈D，将x1反馈回输入端，再输出x2=f(x1 )，并依此规律继续下去，现定义f(x)=(4x-2)/(x+1). （Ⅰ）若输入x0=49/65，则由数列发生器产生数列{xn }，请写出数列{xn }的所有项；（Ⅱ）若要数列发生器生产一个无穷的常数数列，试求输入的初始数据x0的值.（Ⅲ）若输入x0时，产生的无穷数列{xn }满足：对任意正整数n，均有xn<xn+1，求x0的取值范围.

2010年上海世博会园区每天9:00开园，20:00停止入园.在下面的框图中，S表示上海世博会官方网站在每个整点报道的入园总人数，a表示整点报道前1个小时内入园人数，则空白的执行框内应填入__________.

已知 1, 2, a, b 的中位数是 3, 平均数是 4, 则 ab =______.

随机变量ξ的概率分布律由下表给出: 该随机变量ξ的均值是______.

“x=2kπ+π/4（k∈Z）”是“tanx=1 ”成立的【】

已知 x, y 满足,求 z = y − 2x 的最大值为________.