高中数学-高考试题(北京大学 1917年解方程)

计算题（1917年北京大学）

试解一次联立方程式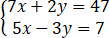

答案解析

①×3+②×2得：31x=155，解得x=5,

代入①式，7×5+2y=47，解得y=6.

∴原方程组的解为.

讨论

高中数学

有酒两种，甲种4升与乙种5升价值之比若 6:7，今甲种4升瓶 26 瓶之价为13元，问乙种 3升瓶 28 瓶该价若干?

鸡犬共若干只，足数共三百二十，而鸡之头数为犬之头数之七分之二，问鸡犬各有几只.

定义椭圆x2/a2 +y2/b2 =1的辅助圆为x2+y2=a2.考虑椭圆x2/4+y2/3=1，点H(a,0),0<a<2. 在第一象限内，过H平行于y轴的直线与椭圆交于点E，与椭圆的辅助圆交于点F，椭圆在点E处的切线与x轴正半轴交于点G，过原点和F的直线与x轴正半轴的夹角为φ.列Ⅰ 列Ⅱ(Ⅰ)若φ=π/4，则△FGH的面积为 (P) (√3-1)4/8(Ⅱ)若φ=π/3，则△FGH的面积为 (Q) 1(Ⅲ)若φ=π/6，则△FGH的面积为 (R) 3/4(Ⅳ)若φ=π/12，则△FGH的面积为 (S) 1/(2√3) (T) (3√3)/2正确的选项为【】

非零实数p,q,r分别为调和数列的第10、第100和第1000项，考虑线性方程组列Ⅰ 列Ⅱ(Ⅰ)若q/r=10，则方程组 (P) 有解x=0,y=10/9,z=-1/9(Ⅱ) 若p/r≠100，则方程组 (Q) 有解x=10/9,y=-1/9,z=0(Ⅲ) 若p/q≠10，则方程组 (R) 无穷多解(Ⅳ) 若p/q=10，则方程组 (S) 无解 (T)至少1个解正确的选项为【】

假设P1,P2两人进行比赛，每回合两人分别投掷一枚均匀的骰子，设x,y分别为P1,P2投出的点数，若x>y，记P1得5分，P2得0分；若x=y，记P1,P2均得2分；若x<y，记P1得0分，P2得5分.设Xi,Yi分别为第i回合后P1,P2的总得分.列Ⅰ 列Ⅱ(Ⅰ)P(X2≥Y2 )= (P) 3/8(Ⅱ)P(X2>Y2 )= (Q) 11/16(Ⅲ)P(X3=Y3 )= (R) 5/16(Ⅳ)P(X3>Y3 )= (S) 355/864 (T) 77/432正确的选项为【】

考虑下面2列，选择正确的选项【】列Ⅰ 列Ⅱ(Ⅰ) {x∈[-2π/3,2π/3]:cosx+sinx=1} (P)有2个元素(Ⅱ) {x∈[-5π/18,5π/18]:√3 tan3x=1} (Q)有3个元素(Ⅲ) {x∈[-6π/5,6π/5]:2cos2x=√3} (R)有4个元素(Ⅳ) {x∈[-7π/4,7π/4]:sinx-cosx=1} (S)有5个元素 (T)有6个元素

定义方程g:[0,π/2]→R为g(θ)=+，其中f(θ)=1/2 +设一元二次函数p(x)的根为方程g(θ)的最大值与最小值，若p(2)=2-√2，则以下说法正确的是【】

设S为抛物线y2=4x的焦点，过点P(-2,1)做抛物线的切线，切点分别为P1与P2，线段SP1上的点Q1与线段SP2上的点Q2满足PQ1⊥SP1,PQ2⊥SP2，则以下说法正确的是【】

设点Q关于平面r➝=-(t+p) i➝+tj➝+(1+p)k➝的对称点为S，其中t,p为实数，i➝,j➝,k➝分别为空间坐标系坐标轴正方向的三个单位向量，若点Q与S的位置矢量分别为10i➝+15j➝+20k➝与αi➝+βj➝+γk➝，则以下说法正确的是【】

已知平面P1:10x+15y+12z-60=0,P2:-2x+5y+4z-20=0.若存在一个四面体，其中两个面分别位于平面P1和P2上，下面哪条直线可能是该四面体的一条棱【】

解方程

武汉大学解方程

解方程x5-1=0.

齐鲁大学解方程

设α,β为x²+mx+m²+a=0的二根，则α²+αβ+β²+a=0.

设a,b,c为方程x³+2x²+3x+4=0之根，求以a(1/b+1/c),b(1/c+1/a),c(1/a+1/b)为根之方程.

问下列联立方程，除x=y=z=0外，是否有其它解存在？如有，将解求出：

解方程组，并详细讨论之.

方程(x5-5x+k)=0有______个实根.

若f(x)=x5+px+q有有理根，且正整数p,q不大于100，则满足条件的(p,q)共有几组.

求19x+93y=4xy的整数解的组数.

函数

定义在区间(-∞,+∞)上的奇函数f(x)为增函数；偶函数g(x)在区间├ [0,+∞)上的图像与f(x)的图像重合.设a>b>0,给出下列不等式：①f(b)-f(-a)>g(a)-g(-b)；②f(b)-f(-a)<g(a)-g(-b)；③f(a)-f(-b)>g(b)-g(-a)；④f(a)-f(-b)>g(b)-g(-a).其中成立的是【】

函数y=a|x| (a>1)的图像是【】

函数f(x)=1/x (x≠0)的反函数f-1 (x)=【】

设曲线C的方程是y=x3 - x，将C沿x轴，y轴正向分别平行移动t,s单位长度后得曲线C1.(Ⅰ)写出曲线C1的方程；(Ⅱ)证明曲线C与C1关于点A(t/2,s/2)对称；(Ⅲ)如果曲线C与C1有且仅有一个公共点，证明s=t3/4 - t且t≠0.

若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0，则g(b)等于【】

已知f(x)=2x+b的反函数为f-1(x),若y=f-1(x)的图像经过点Q(5,2),则b=______.

设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图像为如图所示的线段AB,则在区间[1,2]上,f(x)=__________.

设f(x),g(x)都是单调函数,有如下四个命题：①若f(x)单调递增, g(x)单调递增，则f(x)-g(x)单调递增;②若f(x)单调递增, g(x)单调递减，则f(x)-g(x)单调递增;③若f(x)单调递减, g(x)单调递增，则f(x)-g(x)单调递减;④若f(x)单调递减, g(x)单调递减，则f(x)-g(x)单调递减;其中，正确的命题是【】

设f(x)是定义R上的偶函数，其图像关于直线x=1对称，对任意x_1,x_2∈[0,1/2]，都有f(x1+x2 )=f(x1)f(x2)，且f(1)=a>0.（Ⅰ）求f(1/2)及f(1/4)；（Ⅱ）证明f(x)是周期函数；（Ⅲ）记an=f(2n+1/2n)，求 (lnan).

函数y=2-x+1(x>0)的反函数是【】