设f(x)是定义R上的偶函数,其图像关于直线x=1对称,对任意x_1,x_2∈[0,1/2],都有
f(x1+x2 )=f(x1)f(x2),且f(1)=a>0.
(Ⅰ)求f(1/2)及f(1/4);
(Ⅱ)证明f(x)是周期函数;
(Ⅲ)记an=f(2n+1/2n),求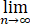 (lnan).
(lnan).
设f(x)是定义R上的偶函数,其图像关于直线x=1对称,对任意x_1,x_2∈[0,1/2],都有
f(x1+x2 )=f(x1)f(x2),且f(1)=a>0.
(Ⅰ)求f(1/2)及f(1/4);
(Ⅱ)证明f(x)是周期函数;
(Ⅲ)记an=f(2n+1/2n),求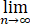 (lnan).
(lnan).
(Ⅰ)因为对x1,x2∈[0,1/2],都有f(x1+x2 )=f(x1 )f(x2 ),所以f(x)=f(x/2)f(x/2)≥0,x∈[0,1].∵f(1)=f(1/2+1/2)=f(1/2)f(1/2)=[f(1/2)]2,f(1/2)=f(1/4+1/4)=f(1/4)f(1/4)=[f(1/4)]2.f(1)=a>0,∴f(1/2)=a1/2,f(1/4)=a1/4.(Ⅱ)依题设y=f(x)关于直线x=1对称,故f(x)=f(1+1-x),即f(x)=f(2-x),x∈R又由f(x)是偶函数知f(-x)=f(x),x∈R∴f(-x)=f(2-x),x...
查看完整答案设函数 f(x) = x3 − 1/x3 , 则 f(x)【 】
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,如果 f(x)=lg(10x+1),x∈(-∞,+∞),那么【 】
设f(x)是(-∞,+∞)上的奇函数, f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于【 】
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图像为如图所示的线段AB,则在区间[1,2]上,f(x)=__________.
已知函数 和g(x)=ax-lnx有相同的最小值.(1)求a;(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.
若函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)f(y),f(1)=1,则f(k)=【 】
已知函数f(x)=ex/x-lnx+x-a.(1)若f(x)≥0,求a的取值范围;(2)证明:若f(x)有两个零点x1,x2,则x1x2<1.
[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【 】
等差数列{an},{bn}的前n项和分别为Sn与Tn,若Sn/Tn =2n/(3n+1),则an/bn 等于【 】
等比数列{an}的首项a1=-1,前n项和为Sn,若S10/S5 =31/32,则Sn 等于【 】
已知数列{an },{bn }都是由正数组成的等比数列,公比分别为p,q,其中p>q且p≠1,q≠1,设cn= an+bn,Sn为数列{cn}的前n项和.求Sn/Sn-1 .
在等比数列{an}中,a1>1,且前n项和Sn满足Sn=1/a1 ,那么a1的取值范围是【 】