若函数f(x)=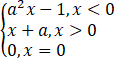
为奇函数，求参数a的值为________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
填空题（2022年上海市）
答案解析
1
【解析】
代入特值求解，利用f(-1)=-f(1)即-a2-1=-(1+a)，解得a=0或a=1，
经检验a=0不符合题意，舍去，
所以，a=1.
讨论
已知函数f(x)及其导函数 的定义域均为R，记g(x)=f' (x)，若f(3/2-2x)，g(2+x)均为偶函数，则【 】
已知函数 和g(x)=ax-lnx有相同的最小值．（1）求a；（2）证明：存在直线y=b，其与两条曲线y=f(x)和y=g(x)共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．
若函数f(x)的定义域为R，且f(x+y)+f(x-y)=f(x)f(y),f(1)=1，则f(k)=【 】
已知函数f(x)=ex/x-lnx+x-a．（1）若f(x)≥0，求a的取值范围；（2）证明：若f(x)有两个零点x1,x2，则x1x2<1．
己知函数f(x)=1/(1+2x)，则对任意实数x，有【 】
已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.
设函数 f(x) = ln|2x + 1| − ln|2x − 1|, 则 f(x)【 】
设函数 f(x) = x3 − 1/x3 , 则 f(x)【 】
已知函数 f(x) = x3 − kx + k2.(1) 讨论 f(x) 的单调性;(2) 若 f(x) 有三个零点, 求 k 的取值范围.
若定义在 R 的奇函数 f(x) 在 (−∞, 0) 单调递减, 且 f(2) = 0, 则满足 xf(x − 1) ⩾ 0 的 x 的取值范围是【 】
已知 y = f(x) 是奇函数, 当 x ⩾ 0 时, f(x) = x2/3 , 则 f(−8) 的值是______.
下面给出的函数中，哪一个函数既是区间(0,π/2)上的增函数，又是以π为周期的偶函数【 】
F(x)=(1+)f(x)(x≠0)是偶函数，且f(x)不恒等于零，则f(x)【 】
已知函数f(x)=x3(a∙2x - 2-x)是偶函数，则a=__________.
设函数f(x)的定义域为R,f(x+1)为奇函数，f(x+2)为偶函数，当x∈[1,2]时，f(x)=ax2+b，若f(0)+f(3)=6，则f(9/2)=【 】
记f(x)是定义域为R的奇函数，且f(1+x)=f(-x)，若f(-1/3)=1/3，则f(5/3)=【 】
设函数f(x)=(1-x)/(1+x)，则下列函数中为奇函数的是【 】