高中数学-高考试题(安徽省 1977年代数式)

计算题（1977年安徽省）

化简

答案解析

暂无答案

讨论

高中数学

安徽省代数式

(tg(-120°)∙cos⁡(-240°)∙cos480°)/(tg(-60°)∙sin⁡(-105°))

(2lg2+lg3)/(2+lg0.36+2/3 lg8)

(-)0+4-2×()-1/2 - (0.01)0.5

安徽省基本初等函数

×(-6/11)+0.25-(-2)3÷(-)2.

设a,b为实数，且a>1，函数f(x)=ax-bx+e2 (x∈R)(1)求函数f(x)的单调区间；(2)若对任意b>2e2，函数f(x)有两个不同的零点，求a的取值范围；(3)当a=e时，证明：对任意b>2e4，函数f(x)有两个不同的零点x1,x2，满足：x2>blnb/(2e2 ) x1+e2/b. (注：e=2.71828… 是自然对数的底数)

如图，已知F是抛物线y2=2px(p>0)的焦点，M是抛物线的准线与x轴的交点，且|MF|=2. (1)求抛物线的方程；(2)设过点F的直线交抛物线于A,B两点，斜率为2的直线l与MA,MB,AB,x轴依次交于点P,Q,R,N，且|RN|2=|PN|∙|QN|，求直线l在x轴上截距的范围.

已知数列{an}的前n项和为Sn,a1=-9/4，且4Sn+1=3Sn-9.(1)求数列{an}的通项；(2)设数列{bn}满足3bn+(n-4) an=0，记{bn}的前n项和为Tn，若Tn<λbn对任意n∈N*恒成立，求λ的范围.

如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点PD⊥DC,PM⊥MD. (1)证明：AB⊥PM;(2)求直线AN与平面PDM所成角的正弦值.

线性代数

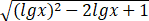
求所有的n∈N*，使得存在n阶实矩阵A,B，满足对任意的n维非零实向量v,Av,Bv线性无关.

给定素数p和正整数 n(n≥2).A为n个p阶循环群的直和.问:至少需要几个A的真子群,才能使他们的并集能覆盖A？

复矩阵A与A的任意正整数次常相似.(1)证明:A的特征值为0或 1;(2)求A的若当标准型.

若下式(x+p)(x+2q)+(x+2p)(x+q)为含有x的整平方式，则9p²-14pq+9q²=0.

河北工业大学行列式

A polynomial P with integer coefficients is square-free if it is not expressible in the form P=Q² R, where Q and R are polynomials with integer coefficients and Q is not constant. For a positive integer n, let Pn be the set of polynomials of the form1+a1 x+a2 x²+⋯+an xnwith a1,a2,⋯,an∈{0,1}. Prove that there exists an integer N so that, for all integers n>N, more than 99% of the polynomials in Pn are square-free.【译】我们称整系数多项式P是无平方因子的，如果其不能表示为P=Q² R的形式，这里Q,R为整系数多项式且Q不为常数.对于正整数n，记Pn为如下形式的多项式组成的集合：1+a1 x+a2 x²+⋯+an xn这里a1,a2,⋯,an∈{0,1}.证明：存在整数N，使得对任意的整数n≥N,Pn中超过99%的多项式都是无平方因子的.

令A,B,C,D,E,F是三阶实方阵，且=.已知A=,B=且C=A+B-I，则[|detF|]=______.

设20阶实矩阵A满足eA=I20，且A在复数域上的所有特征值模长均不超过20，则这样的互不相似的A有______个.

有理数加群(Q,+)，记所有分母不超过10的有理数构成的子集为G，其对应的陪集GZ记为G ̅，则Q/Z包含G ̅的最小子群的阶为______.

代数式

分解因式：x2-4xy+4y2-4z2.

甲乙两容器内都盛有酒精，甲有v1公斤，乙有v2公斤.甲中纯酒精与水（重量）之比为m1:n1，乙中纯酒精与水之比为m2:n2，问将二者混合后所得液体中纯酒精与水之比是多少？

将多项式x5y-9xy5分别在下列范围内分解因式：1. 有理数范围； 2. 实数范围；3. 复数范围．

如果n是正整数，那么1/8[1-(-1)n](n2-1)的值【】

已知正整数n,恰有36个不同的质数整除n，对k=1,2,3,4,5，记[(k-1)n/5,kn/5]中互质的整数个数为Cn，已知C1,C2,C3,C4,C5不完全相同.求证：(Ci - Cj)2 ≥236.

解明：(6x+5)/(8x-15)-(1+8x)/15=(1-x)/3+(3-x)/5

设a:b = x:y，试证 (a³ + 2b³) : ab² = (z³ +2y³) : xy².

变换方程式x4+16x3+89x2+200x+156=0，使其缺第二项,因而求原方程式之根.

若多项式 f(x) 之系数皆为整数，且 f(0) 及 f(1) 又均为奇数，试证 f(x) = 0绝无整数根.

分解因式 x4-23x2+1