已知正整数n,恰有36个不同的质数整除n,对k=1,2,3,4,5,记[(k-1)n/5,kn/5]中互质的整数个数为Cn,已知C1,C2,C3,C4,C5不完全相同.
求证: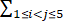 (Ci - Cj)2 ≥236.
(Ci - Cj)2 ≥236.
已知正整数n,恰有36个不同的质数整除n,对k=1,2,3,4,5,记[(k-1)n/5,kn/5]中互质的整数个数为Cn,已知C1,C2,C3,C4,C5不完全相同.
求证: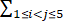 (Ci - Cj)2 ≥236.
(Ci - Cj)2 ≥236.
不妨设n=p1 p2…p36.定义f(n)=([n/5],[2n/5]-[n/5],[3n/5]-[2n/5],[4n/5]-[3n/5],[5n/5]-[4n/5]),若n=0,则f(0)=(0,0,0,0,0),可忽略.约定∀k∈R (a1+k,a2+k,a3+k,a4+k,a5+k)=(a1,a2,a3,a4,a5 )所以,若a≡b(mod5),则f(a)=f(b)设A=(c1,c2,c3,c4,c5 )=f(n)-[(f(n/p1 )+f(n/p2 )+⋯)]+[(f(n/(p1 p2 ))+⋯)]若n不为5的倍数,设n≡,1/pi ≡ (mod 5),定义g(x)=f(2x),则g(x+4)=g(x).则A=g(a0 )-[g(a0+a1 )+g(a0+a2 )+⋯]+[g(a0+a1+a2 )+⋯]取h(x)= (-1)(-1)…(-1)=(x-1)d (x2-1)e (x3-1)f (x4-1)g=-(++⋯)+(+⋯) 于是A中g(t)(t=1,2,3,4)的个数为a0,a0+a1,a0+a2,…中≡(mod 4)的个数,[注:①g(4k+t)视为g(t);② 若a0+ai≡t(mod 4),视作“-1”个”“ ≡t(mod ...
查看完整答案设椭圆的中心是坐标原点,长轴在x轴上,离心率e=/2,已知点P(0,3/2)到这个椭圆上的点的最远距离是.求这个椭圆的方程,并求椭圆上到点P的距离等于的点的坐标.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.
已知sinα+sinβ=1/4,cosα+cosβ=1/3,求tan(α+β)的值.
有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数.
如图,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1:V2=__________.
解明:(6x+5)/(8x-15)-(1+8x)/15=(1-x)/3+(3-x)/5
设a:b = x:y,试证 (a³ + 2b³) : ab² = (z³ +2y³) : xy².
某学生带银去买书籍等物; 要用所有银的1/4买字典,1/5买地理,1/6买文具,这样算,付价之后,还可以剩银23/10元; 问他带去银是多少?
变换方程式x4+16x3+89x2+200x+156=0,使其缺第二项,因而求原方程式之根.
若多项式 f(x) 之系数皆为整数,且 f(0) 及 f(1) 又均为奇数,试证 f(x) = 0绝无整数根.
Simplify yz(x+a)/(x-y)(x-z)+zx(y+a)/(y-z)(y-x)+xy(z+a)/(z-x)(z-y)