高中数学-高考试题(全国统考 1990年椭圆)

问答题（1990年全国统考）

设椭圆的中心是坐标原点，长轴在x轴上，离心率e=/2，已知点P(0,3/2)到这个椭圆上的点的最远距离是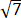.求这个椭圆的方程，并求椭圆上到点P的距离等于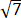的点的坐标.

答案解析

设所求椭圆的直角坐标方程是x2/a2 +y2/b2 =1,其中a>b>0由e2=c2/a2 =(a2-b2)/a2 =1-(b/a)2可得b/a===1/2，即a=2b.设椭圆上的点(x,y)到点P的距离为d，则d2=x2+(y-3/2)2 =a2 (1-y2/b2 )+y2-3y+9/4 =4b2-3y2-3y+9/4 =-3(y+1/2)2+4b2+3,其中-b≤y≤b.如果b<...

查看完整答案

讨论

圆锥曲线

求曲线y2=-16x+64的焦点.

过点M(-1,0)的直线l1与抛物线y2=4x交于P1,P2两点.记：线段P1P2的中点这P；过点P和这个抛物线的焦点F的直线为l2；l1的斜率为k.试把直线l2的斜率与直线l1的斜率之比表示为k的函数，并指出这个函数的定义域、单调区间，同时说明在每一单调区间上它是增函数还是减函数.

在抛物线y=4x2上求一点，使该点到直线y=4x-5的距离最短.

定长为3的线段AB的两个端点在抛物线y2=x上移动，记线段AB的中点为M.求点M到y轴的最短距离，并求此时点M的坐标.

设椭圆x2/a2 +y2/b2 =1(a>b>0)的右焦点为F1右准线为l1.若过F1且垂直于x轴的弦的长等于点F1到l1的距离，则椭圆的离心率是________.

双曲线x2/9 - y2/16=1的两个焦点为F1,F2，点P在双曲线上.若PF1⊥PF2，则点P到x轴的距离为________.

在平面直角坐标系xOy中，已知点F1(-,0),F2 (,0)，点M满足：|MF1|-|MF2|=2.记M的轨迹为C.(1)求C的方程；(2)设点T在直线x=1/2上，过T的两条直线分别交C于A,B两点和P,Q两点，且|TA|∙|TB|=|TP|∙|TQ|，求直线AB的斜率与直线PQ的斜率之和.

已知F1,F2是双曲线C的两个焦点，P为C上一点，且∠F1PF2=60°,|PF1|=3|PF2|，则C的离心率为【】

已知双曲线x2/a2 -y2/b2 =1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合，抛物线的准线交双曲线于A、B两点，交双曲线的渐近线与C、D两点,若|CD|=√2|AB|，则双曲线的离心率为【】

求椭园25x2+9y2=100的长轴和短轴的长、焦点坐标，并且画出它的图像。

椭圆

已知椭圆x2/6+y2/3=1，直线l与椭圆在第一象限交于A，B两点，与x轴，y轴分别交于M，N两点，且|MA|=|NB|,|MN|=2√3，则直线l的方程为___________．

椭圆C:x2/a2 +y2/b2 =1(a>b>0)的左顶点为A，点P，Q均在C上，且关于y轴对称．若直线AP,AQ的斜率之积为1/4，则C的离心率为【】

已知Γ:x2/a2 +y2/b2 =1(a>b>0)的左、右焦点分别为F1 (-√2,0),F2 (√2,0),A为Γ的下顶点，M为直线l:x+y-4√2=0上一点.(1)若a=2,AM的中点在x轴上，求点M的坐标；(2)直线l交y轴于点B，直线AM经过点F2，若△ABM有一个内角的余弦值为3/5，求b；(3)若椭圆Γ上存在点P到直线l的距离为d，且满足d+|PF1 |+|PF2 |=6，当a变化时，求d的最小值.

已知常数a>0，在矩形ABCD中，AB=4,BC=4a,O为AB的中点，点E,F,G分别在BC,CD,DA上移动，且BE/BC=CF/CD=DG/DA,P为GE与OF的交点(如图).问是否存在两个定点，使P到这两点的距离的和为定值?若存在，求出这两点的坐标及此定值;若不存在，请说明理由.

已知椭圆方程x2/a2 +y2/b2 =1,F为右焦点，A为右顶点，B为上顶点，|BF|/|AB| =√3/2.(1)求椭圆的离心率e；(2)已知直线l与椭圆有唯一交点M，直线l交y轴于点N,|OM|=|ON|,∆OMN的面积为√3,求椭圆的标准方程.

Find the area of the triangle out off from the first quadrant by the tangent to the ellipse 2x² + 3y² = 14 at the point (1, 2).

设P点在椭圆所引之二切线与其长轴之夹角为θ1,θ2，试就下列情形分别求P之轨迹.(1).tanθ1+tanθ2 为一定值.(2).cotθ1+cotθ2 为一定值.

椭圆x2/a2 +y2/b2 =1上三点P,Q,R之离心角顺次为θ,ϕ,φ，试示P,Q,R处三切线所成三角形之面积（不计符号）为abtan (θ-ϕ)/2 tan (θ-φ)/2 tan (φ-θ)/2

试求经过二曲线 x²+2y² - 4x - 2y -6 =0及y² +xy-8 =0之交点且与x轴相切之圆锥曲线方程式.

设 P 为圆上之任意点，且 F 为一焦点，证明以 FP 及椭圆之长轴各为直径之圆必相内切.

平面解析几何

已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .

如果圆x2+y2+Gx+Ey+F=0与x轴相切于原点，那么【】。

在△ABC中，∠A,∠B,∠C所对的边分别为a,b,c,且c=10, cosA/cosB=b/a=4/3, P为△ABC的内切圆上的动点.求点P到顶点A,B,C的距离的平方和的最大值与最小值.

圆C：x2+y2-2x-4y+4=0的圆心到直线3x+4y+4=04的距离d=_____.

如果方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)所表示的曲线关于y=x对称，那么必有【】

设圆M的方程为(x-3)2+(y-2)2=2，直线l的方程为x+y-3=0，点P的坐标为(2,1)，那么【】

如果实数x,y满足等式(x-2)2+y2=3，那么y/x的最大值是【】

记△ABC的内角A,B,C的对边分别为a,b,c，已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.(1)证明：BD=b；(2)若AD=2DC，求cos∠ABC.

在△ABC中，已知a=3,b=2c.(1)若A=2π/3，求S△ABC.(2) 若2sinB-sinC=1，求C△ABC.

若斜率为√3的直线与y轴交于点A，与圆x2+(y-1)2=1相切与点B，则|AB|=_______.