已知双曲线方程x2/20-y2/5=1，那么它的焦距是【 】
A、10
B、5
C、2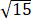
D、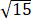
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设B是椭圆C:x2/a2 +y2/b2 =1(a>b>0)的上顶点，若C上的任意一点P都满足|PB|≤2b，则C的离心率取值范围是【 】
设B是椭圆C:x2/5+y2=1的上顶点，点P在C上，则|PB|的最大值为【 】
已知椭圆短轴长为2，中心与抛物线y2=4x的顶点重合，椭圆的一个焦点恰是此抛物线的焦点，求椭圆方程及其长轴的长。
已知菱形的一对内角各为60°，边长为4，以菱形对角线所在的直线为坐标轴建立直角坐标系，以菱形60°角的两个顶点为焦点，并且过菱形的另外两个顶点作椭圆，求椭圆方程.
已知椭圆x2/16+y2/4=1的左右焦点分别为F1与F2，点P在直线l:x-√3 y+8+2√3=0上.当∠F1 PF2取最大值时，比|PF1 |/(|PF2 |)的值为____________.
双曲线上一点与其两渐近线之阿离如何？并证此两距离相乘之积为常数.
过原点作直线垂直于双曲线 x²-y² = a² 上一切线，求垂足之轨迹之极坐标方程.
已知双曲线C的焦点为(-2,0)和(2,0)，离心率为√2，则C的方程为____________.
设双曲线x²/a² -y²/b² =1(a>0,b>0)的左右焦点分别为F1,F2，过F2作平等于y轴的直线交C于A,B两点，若|F1A|=13,|AB|=10，则C的离心率为______.
设 F1, F2 是双曲线 C : x2 −y2/3 = 1 的两个焦点, O 为坐标原点, 点 P 在 C 上且 |OP| = 2, 则 △PF1F2 的 面积为【 】
已知方程x2/(2+λ)-y2/(1+λ)=1表示双曲线，求λ的取值范围.
双曲线x2/9 - y2/16=1的两个焦点为F1,F2，点P在双曲线上.若PF1⊥PF2，则点P到x轴的距离为________.
已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1)，则|a→ |²-|b→ |²=【 】
在△ABC中，(a+c)(sinA-sinC)=b(sinA-sinB)，则∠C=【 】
已知向量|a➝ |=1,|b➝ |=2，且a➝,b➝的夹角为120°.若a➝+tb➝与ta➝+b➝的夹角为锐角，则t的取值范围是__________.
已知在△ABC中，a=2b,cosB=2√2/3，则sin(A-B)/2+sinC/2=__________.
在△ABC中，AB=1,AC=2,B-C=2π/3，则△ABC的面积为__________.
已知圆 x2 + y2 −6x = 0, 过点 (1,2) 的直线被该圆所截得的弦的长度的最小值为【 】
设向量 a = (1, −1), b = (m + 1, 2m − 4), 若 a ⊥ b, 则 m =______ .