设B是椭圆C:x2/5+y2=1的上顶点,点P在C上,则|PB|的最大值为【 】
A、5/2
B、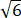
C、
D、2
已知椭圆x2/a2 +y2/b2 =1(a>b>0),A,B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明:-(a2 - b2)/a < x0 < (a2 - b2)/a.
如图,在面积为1的△PMN中,tanM=1/2,tanN=-2.建立 适当的坐标系,求出以M,N为焦点且过点P的椭圆方程.
如果方程x2 + ky2 = 2表示焦点在y轴上的椭圆,那么实数k的取值范围是【 】
椭圆C与椭圆(x-3)2/9+(y-2)2/4=1关于直线x+y=0对称,椭圆C的方程是【 】
椭圆x2/12+y2/3=1的焦点为F1和F2,点P在椭圆上.如果线段PF1的中点在y轴上,那么|PF1 |是|PF2 |的【 】
设椭圆x2/a2 +y2/b2 =1(a>b>0)的右焦点为F1右准线为l1.若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是________.
如图,给出定点A(a,0)(a>0)和直线l:x=-1.B是直线l上的动点,∠BOA的平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
椭圆x2/9+y2/4=1的焦点为F1,F2,点P为其上的动点.当∠F1PF2为钝角时,点P横坐标的取值范围是____________.
已知椭圆C的焦点分别为F1(-2,0)和F2(2,0),长轴长为6,设直线y=x+2交椭圆C于A,B两点,求线段AB的中点坐标.
若椭圆经过原点,且焦点为F1(1,0),F2(3,0),则其离心率为【 】
设F1,F2为椭圆x2/9+y2/4=1的两个焦点,P为椭圆上的一点.已知P,F1,F2是一个直角三角形的上顶点,且|PF1|>|PF2|,求|PF1|/|PF2| 的值.
已知椭圆x2/2+y2=1的右准线l与x轴相交于点E,过椭圆右焦点F的直线与椭圆相交于A,B两点,点C在右准线l上,且BC//x轴.求证直线AC经过线段EF的中点.
已知F1,F2是椭圆C:x2/9+y2/4=1的两个焦点,点M在C上,则|MF1|∙|MF2|的最大值为【 】
已知F1,F2为椭圆C:x2/16+y2/4=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2 |,则四边形PF1QF2的面积为________.
设B是椭圆C:x2/a2 +y2/b2 =1(a>b>0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率取值范围是【 】
椭圆C:x2/a2 +y2/b2 =1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为1/4,则C的离心率为【 】
已知椭圆C:x2/a2 +y2/b2 =1(a>b>0)的离心率为1/3,A1,A2分别为C的左、右顶点,B为C的上顶点.若(BA1)⋅(BA2)=-1,则C的方程为【 】
如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a=【 】
设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3 : 1,在满足条件①②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
设圆过双曲线x2/9 - y2/16=1的一个顶点和-一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是________.
直线x + y - 2 = 0截圆x2 + y2 = 4得到的劣弧所对的圆心角为【 】
过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是【 】
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是【 】
设A,B是x轴上的两点,点P的横坐标为2且|PA|=|PB|.若直线PA的方程为x-y+1=0,则直线PB的方程是【 】
已知a,b,c是△ABC中∠A,∠B,∠C的对边,S是△ABC的面积,若a=4,b=5,S=5,求c的长度.
已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则【 】
记△ABC的内角A,B,C的对边分别为a,b,c,已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.(1)证明:BD=b;(2)若AD=2DC,求cos∠ABC.