如图,给出定点A(a,0)(a>0)和直线l:x=-1.B是直线l上的动点,∠BOA的平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
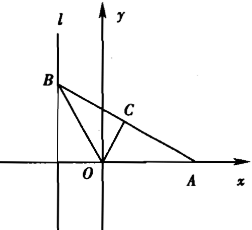
如图,给出定点A(a,0)(a>0)和直线l:x=-1.B是直线l上的动点,∠BOA的平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.

依题意,记B(-1,b),(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.设点C(x,y),则有0≤x<a,由OC平分∠AOB,知点C到OA,OB距离相等.根据点到直线的距离公式得|y|=|y+bx|/.①依题设,点C在直线AB上,故由有y=-b/(1+a) (x-a).由x-a≠0,得b=-(1+a)y/(x-a).②将②式代入①式得y2 [1+ ]=[y-]2,整理得y2 [(1-a) x2-2ax+1(1+a) y2 ]=0,若y...
查看完整答案设O为坐标原点,直线y=-√3(x-1)过抛物线C:y²=2px(p>0)的焦点,且与C交于M,N两点,l为C的准线,则【 】
已知抛物线C:y²=8x的焦点为F,点M在C上.若M到直线x=-3距离为5,则|MF|=【 】
已知 A 为抛物线 C : y2 = 2px(p > 0) 上一点, 点 A 到 C 的焦点的距离为 12, 到 y 轴的距离为 9, 则 p=【 】。
设 O 为坐标原点, 直线 x = 2 与抛物线 C : y2 = 2px (p > 0) 交于 D, E 两点, 若 OD ⊥ OE, 则 C 的焦点坐标为【 】
斜率为 的直线过抛物线 C : y2 = 4x 的焦点, 且与 C 交于 A, B 两点, 则 |AB| =______.
设抛物线的顶点为 O, 焦点为 F , 准线为 l. P 是抛物线上异于 O 的一点, 过 P 作 PQ ⊥ l 于 Q, 则线段 FQ 的垂直平分线【 】
设F1和F2为双曲线x2/4 - y2 = 1的两个焦点,点P在双曲线上且满足∠F1PF2 = 90°,则△F1PF2的面积是【 】
设双曲线x2/a2 - y2/b2 =1(0<a<b)的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为/4 c,则双曲线的离心率为【 】
若双曲线y2-x2/m2 =1(m>0)的渐近线与圆x2+y2-4y+3=0相切,则m=_________.
记双曲线C:x2/a2 -y2/b2 =1(a>0,b>0)的离心率为e,写出满足条件“直线y=2x与C无公共点”的e的一个值_________.
双曲线C的两个焦点为F1,F2,以C的实轴为直径的圆记为D,过F1作D的切线与C的两支交于M,N两点,且cos∠F1NF2=3/5,则C的离心率为【 】
已知双曲线y2+x2/m=1的渐近线方程为y=±√3/3 x,则m=__________.
求经过定点M(1,2),以y轴为准线,离心率为1/2的椭圆的左顶点的轨迹方程.
设椭圆方程为x2/a2 +y2/b2 =1(a>b>0),令c=,那么它的准线方程为【 】
设椭圆的中心是坐标原点,长轴在x轴上,离心率e=/2,已知点P(0,3/2)到这个椭圆上的点的最远距离是.求这个椭圆的方程,并求椭圆上到点P的距离等于的点的坐标.
椭圆C与椭圆(x-3)2/9+(y-2)2/4=1关于直线x+y=0对称,椭圆C的方程是【 】
椭圆x2/12+y2/3=1的焦点为F1和F2,点P在椭圆上.如果线段PF1的中点在y轴上,那么|PF1 |是|PF2 |的【 】
设椭圆x2/a2 +y2/b2 =1(a>b>0)的右焦点为F1右准线为l1.若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是________.