已知Γ:x2/2+y2=1,F1,F2是其左、右焦点,直线l过点P(m,0)(m≤- ),交椭圆于A,B两点,且A,B在x轴上方,点A在线段BP上.
),交椭圆于A,B两点,且A,B在x轴上方,点A在线段BP上.
(1)若B是上顶点,|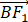 |=|
|=| |,求m的值;
|,求m的值;
(2)若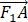 ∙
∙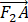 =1/3,且原点O到直线l的距离为4
=1/3,且原点O到直线l的距离为4 /15,求直线l的方程;
/15,求直线l的方程;
(3)证明:对于任意m<- ,使得
,使得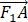 //
//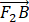 的直线有且仅有一条.
的直线有且仅有一条.
已知Γ:x2/2+y2=1,F1,F2是其左、右焦点,直线l过点P(m,0)(m≤- ),交椭圆于A,B两点,且A,B在x轴上方,点A在线段BP上.
),交椭圆于A,B两点,且A,B在x轴上方,点A在线段BP上.
(1)若B是上顶点,|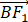 |=|
|=| |,求m的值;
|,求m的值;
(2)若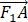 ∙
∙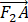 =1/3,且原点O到直线l的距离为4
=1/3,且原点O到直线l的距离为4 /15,求直线l的方程;
/15,求直线l的方程;
(3)证明:对于任意m<- ,使得
,使得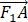 //
//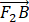 的直线有且仅有一条.
的直线有且仅有一条.
(1)由椭圆方程知a2=2,b2=1,∴c2=a2-b2=1,∴椭圆焦点为:F1 (-1,0),F2 (1,0).若B为椭圆的上顶点,则B(0,1),∴|BF1 |=,∵|BF1 |=|PF1 |,∴=-1-m,解得m=-1-.(2)设点A( cosθ,sinθ),则∙=( cosθ+1)( cosθ-1)+sin2 θ=2cos2 θ-1+sin2 θ=1/3,根据A在线段BP上,横坐标小于0,解得cosθ=-/3,故A(-√6/3,√6/3).设直线l的方程为y=kx+√6/3 k+√6/3(k>0),则原点O到直线l的距离为d==4/15,解得k=3或k=1/3,故直线l的方程为y=1/3 x+(4√6)/9或y=3x+(4√6)/3(不满足m<-,舍...
查看完整答案已知向量|a➝ |=1,|b➝ |=2,且a➝,b➝的夹角为120°.若a➝+tb➝与ta➝+b➝的夹角为锐角,则t的取值范围是__________.
已知向量a ̅=(0,1),b ̅=(2,x),若b ̅⊥(b ̅- 4a ̅),则x=【 】
设向量 a = (1, −1), b = (m + 1, 2m − 4), 若 a ⊥ b, 则 m =______ .
己知单位向量 a, b 的夹角为 45°, ka − b 与 a 垂直, 则 k = ______.
已知单位向量 a, b 的夹角为 60°, 则下列向量中, 与 b 垂直的是【 】
在平面内, A, B 是两个定点, C 是动点. •= 1, 则点 C 的轨迹为【 】
已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则• 的取值范围是【 】
设向量a,b的夹角的余弦值为1/3,且|a|=1,|b|=3,则(2a+b)⋅b=_________.
已知λ>0,向量|a|=|b|=|c|=λ,且a∙b=0,c∙b=1,c∙a=2,则λ=________.
已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .
已知F1,F2为椭圆C:x2/16+y2/4=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2 |,则四边形PF1QF2的面积为________.
设B是椭圆C:x2/a2 +y2/b2 =1(a>b>0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率取值范围是【 】
设B是椭圆C:x2/5+y2=1的上顶点,点P在C上,则|PB|的最大值为【 】
设 P 为圆上之任意点,且 F 为一焦点,证明以 FP 及椭圆之长轴各为直径之圆必相内切.
设椭圆C1:x²/a² +y²=1(a>1),C2:x²/4+y²=1的离心率分别为e1,e2,若e2=√3e1,则a=【 】
已知椭圆C:x²/3+y²=1的左、右焦点分别为F1,F2,直线y=x+m与C交于A,B两点,若△F1AB的面积是△F2AB面积的2倍,则m=【 】
造型 可以做成美丽的丝带,将其看作图中曲线C的一部分.已知C过坐标原点O,且C上的点满足:横坐标大于-2,到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4,则【 】
已知点 O(0, 0), A(−2, 0), B(2, 0). 设点 P 满足 |PA| − |PB| = 2, 且 P 为函数 y=3 图像上的点,则 |OP| =【 】
如图,已知椭圆长轴|A1A2 |=6,焦距|F1F2 |=4,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π),当α取什么值时,|MN|等于椭圆短轴的长?
设F1,F2为椭圆x2/9+y2/4=1的两个焦点,P为椭圆上的一点.已知P,F1,F2是一个直角三角形的上顶点,且|PF1|>|PF2|,求|PF1|/|PF2| 的值.
已知椭圆x2/2+y2=1的右准线l与x轴相交于点E,过椭圆右焦点F的直线与椭圆相交于A,B两点,点C在右准线l上,且BC//x轴.求证直线AC经过线段EF的中点.
已知F1,F2是椭圆C:x2/9+y2/4=1的两个焦点,点M在C上,则|MF1|∙|MF2|的最大值为【 】
椭圆C:x2/a2 +y2/b2 =1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为1/4,则C的离心率为【 】